NE0 Lowest Order Edge Element in 3D

Contents

Data Structure

Use the function

[elem2dof,edge,elem2edgeSign] = dof3edge(elem);

to construct the pointer from element index to edge index. Read Dof on Edges in Three Dimensions for details.

node = [1,0,0; 0,1,0; 0,0,0; 0,0,1];
elem = [1 2 3 4];
localEdge = [1 2; 1 3; 1 4; 2 3; 2 4; 3 4];
figure;
showmesh3(node,elem);
view(114,36);
findnode3(node);
findedge(node,localEdge,'all','vec');

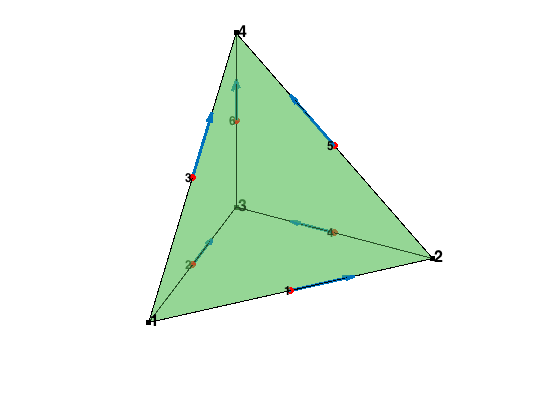
The six dofs associated to edges in a tetrahedron is sorted in the ordering [1 2; 1 3; 1 4; 2 3; 2 4; 3 4]. Here [1 2 3 4] are local indices of vertices.

Globally we use ascend ordering for each element and thus the orientation of the edge is consistent. No need of elem2edgeSign.

Local Bases

Suppose [i,j] is the kth edge and i<j. The basis is given by

$$ \phi _k = \lambda_i\nabla \lambda_j - \lambda_j \nabla \lambda_i,\qquad \nabla \times \phi_k = 2\nabla \lambda_i \times \nabla \lambda_j.$$

Inside one tetrahedron, the 6 bases functions along with their curl corresponding to 6 local edges [1 2; 1 3; 1 4; 2 3; 2 4; 3 4] are

$$ \phi_1 = \lambda_1\nabla\lambda_2 - \lambda_2\nabla\lambda_1,\qquad \nabla \times \phi_1 = 2\nabla\lambda_1\times \nabla\lambda_2,$$

$$ \phi_2 = \lambda_1\nabla\lambda_3 - \lambda_3\nabla\lambda_1,\qquad \nabla \times \phi_2 = 2\nabla\lambda_1\times \nabla\lambda_3,$$

$$ \phi_3 = \lambda_1\nabla\lambda_4 - \lambda_4\nabla\lambda_1,\qquad \nabla \times \phi_3 = 2\nabla\lambda_1\times \nabla\lambda_4,$$

$$ \phi_4 = \lambda_2\nabla\lambda_3 - \lambda_3\nabla\lambda_2,\qquad \nabla \times \phi_4 = 2\nabla\lambda_2\times \nabla\lambda_3,$$

$$ \phi_5 = \lambda_2\nabla\lambda_4 - \lambda_4\nabla\lambda_2,\qquad \nabla \times \phi_5 = 2\nabla\lambda_2\times \nabla\lambda_4,$$

$$ \phi_6 = \lambda_3\nabla\lambda_4 - \lambda_4\nabla\lambda_3,\qquad \nabla \times \phi_6 = 2\nabla\lambda_3\times \nabla\lambda_4.$$


Published with MATLAB® R2014b