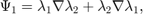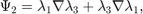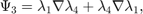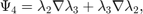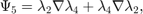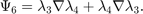NE1 Linear Edge Element in 3D

Data Structure

The second family share the same data structure with the first one; see Lowest order edge element space in 3D.

Suppose [i,j] is the kth edge. The basis for the first family is given by

$\Phi _k = \lambda_i\nabla \lambda_j - \lambda_j \nabla \lambda_i,\qquad \nabla \times \Phi_k = 2\nabla \lambda_i \times \nabla \lambda_j.$

The additional 6 bases for the second family are:

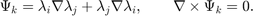
$\Psi _k = \lambda_i\nabla \lambda_j + \lambda_j \nabla \lambda_i,\qquad \nabla \times \Psi_k = 0.$

Inside one tetrahedron, the 6 bases functions along with their curl corresponding to 6 local edges [1 2; 1 3; 1 4; 2 3; 2 4; 3 4] are

$\Psi_1 = \lambda_1\nabla\lambda_2 + \lambda_2\nabla\lambda_1,$

$\Psi_2 = \lambda_1\nabla\lambda_3 + \lambda_3\nabla\lambda_1,$

$\Psi_3 = \lambda_1\nabla\lambda_4 + \lambda_4\nabla\lambda_1,$

$\Psi_4 = \lambda_2\nabla\lambda_3 + \lambda_3\nabla\lambda_2,$

$\Psi_5 = \lambda_2\nabla\lambda_4 + \lambda_4\nabla\lambda_2,$

$\Psi_6 = \lambda_3\nabla\lambda_4 + \lambda_4\nabla\lambda_3.$