Equation: Poisson Equation Discretized by 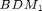Element in 3D

We explain the assembling of the matrix equation for the lowest order BDM element discretization of Poisson equation.

[u,sigma] = Poisson3BDM1(node,elem,bdEdge,f,g_D,varargin)

Created by Ming Wang at Dec 30. 2010.

Data Structure
Local Bases
Mass Matrix
Matrix for Differential Operator
Right hand side

Data Structure

 [elem2dof,dofSign,face] = dof3BDM1(elem);

will construct local to global index map; see ifem dof3BDM1doc for details.

Local Bases

Suppose 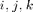$i,j,k$ is the vertices of the $l$ -th face. The basis along with their div are given by

$\phi_l^1 = \lambda_i\nabla \lambda_j \times \nabla\lambda_k,\quad \phi_l^2 = \lambda_j\nabla \lambda_k \times \nabla\lambda_i,\quad \phi_l^3 = \lambda_k\nabla \lambda_i \times \nabla\lambda_j.$

$\nabla \cdot\phi_l^1 = \nabla \cdot\phi_l^2 = \nabla \cdot\phi_l^3 = det(\nabla\lambda_i,\nabla\lambda_j,\nabla\lambda_k).$

Inside one tetrahedron, the 12 bases functions along with their div corresponding to 4 local faces [2 3 4; 1 4 3; 1 2 4; 1 3 2] are:(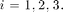 $i=1,2,3.$ )

$\phi_1^1 = \lambda_2\nabla \lambda_3 \times \nabla\lambda_4,\quad \phi_1^2 = \lambda_3\nabla \lambda_4 \times \nabla\lambda_2,\quad \phi_1^3 = \lambda_4\nabla \lambda_2 \times \nabla\lambda_3,\quad \nabla \cdot\phi_1^i = det(\nabla\lambda_2,\nabla\lambda_3,\nabla\lambda_4).$

$\phi_2^1 = \lambda_1\nabla \lambda_4 \times \nabla\lambda_3,\quad \phi_2^2 = \lambda_4\nabla \lambda_3 \times \nabla\lambda_1,\quad \phi_2^3 = \lambda_3\nabla \lambda_1 \times \nabla\lambda_4,\quad \nabla \cdot\phi_2^i = det(\nabla\lambda_1,\nabla\lambda_4,\nabla\lambda_3).$

$\phi_3^1 = \lambda_1\nabla \lambda_2 \times \nabla\lambda_4,\quad \phi_3^2 = \lambda_2\nabla \lambda_4 \times \nabla\lambda_1,\quad \phi_3^3 = \lambda_4\nabla \lambda_1 \times \nabla\lambda_2,\quad \nabla \cdot\phi_3^i = det(\nabla\lambda_1,\nabla\lambda_2,\nabla\lambda_4).$

$\phi_4^1 = \lambda_1\nabla \lambda_3 \times \nabla\lambda_2,\quad \phi_4^2 = \lambda_3\nabla \lambda_2 \times \nabla\lambda_1,\quad \phi_4^3 = \lambda_2\nabla \lambda_1 \times \nabla\lambda_3,\quad \nabla \cdot\phi_4^i = det(\nabla\lambda_1,\nabla\lambda_3,\nabla\lambda_2).$

Locally, we order the local bases in the following way:

$\{\phi_1^1,~\,\phi_2^1,~\,\phi_3^1,~\,\phi_4^1,~\,\phi_1^2,~\,\phi_2^2,~\, \phi_3^2,~\,\phi_4^2,~\,\phi_1^3,~\,\phi_2^3,~\,\phi_3^3,~\,\phi_4^3.\}$

and rewrite the local bases as:

$\{\phi_1,~\,\phi_2,~\,\phi_3,~\,\phi_4,~\,\phi_5,~\,\phi_6,~\, \phi_7,~\,\phi_8,~\,\phi_9,~\,\phi_{10},~\,\phi_{11},~\,\phi_{12}.\}$

Because of the different oritentation of local and global faces, from local bases to the global one, the direction should be corrected. That is

  phiGlobal(elem2dof(t,1),:) = phi(t,1)*dofSign(t,1);

Mass Matrix

We use the integral formula

$\int_T \lambda_1^{\alpha_1}\lambda_2^{\alpha_2}\lambda_3^{\alpha_3}\lambda_4^{\alpha_4} dx = \frac{\alpha_1!\alpha_2!\alpha_3!\alpha_4!3!}{(\sum _{i=1}^4\alpha_i + 3)!}\;|T|,$

to get

$\int _T\lambda_i\lambda_j dx = (1+(i==j))|T|/20.$

In order to calculate the mass matrix, we need to construct a matrix, say, locBasesIdx, to calculate the local index used in the bases. For example, for basis 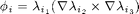$\phi_i =\lambda_{i_1}(\nabla \lambda_{i_2}\times\nabla\lambda_{i_3})$ , we compute 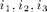$i_1,i_2,i_3$ in the way:

$i1$ = locBasesIdx(i,1); $i2$ = locBasesIdx(i,2); 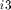$i3$ = locBasesIdx(i,3);

where locBasesIdx are constructed as:

locFace = [2 3 4; 1 4 3; 1 2 4; 1 3 2];
locBasesIdx = [locFace(:,[1 2 3]);locFace(:,[2 3 1]);locFace(:,[3 1 2])];

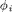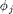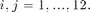
For two local bases $\phi_i$ and $\phi_j$ , $i, j = 1,...,12.$ $\int_T \phi_i \phi_j dx = \int_T ( \lambda_{i_1}\nabla \lambda_{i_2}\times\nabla\lambda_{i_3})\cdot (\lambda_{j_1}\nabla \lambda_{j_2}\times\nabla\lambda_{j_3}) dx.$

Matrix for Differential Operator

We record 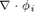$\nabla \cdot \phi_i$ and then the computation 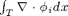$\int _T \nabla \cdot \phi_i dx$ is straightforward. Just remember to correct the direction.

Right hand side

We use 5-points quadrature which is exact for cubic polynomials. In the barycentric coordinate, the 5-points are

$p_1 = [1/4, 1/4, 1/4, 1/4], \quad w_1 = -4/5$

$p_2 = [1/2, 1/6, 1/6, 1/6], \quad w_2 = 9/20$

$p_3 = [1/6, 1/2, 1/6, 1/6], \quad w_3 = 9/20$

$p_4 = [1/6, 1/6, 1/2, 1/6], \quad w_4 = 9/20$

$p_5 = [1/6, 1/6, 1/6, 1/2], \quad w_5 = 9/20$

Note that the two for loops are nested in such a way that the point pxy and the evulation Jp is just computed once.

The local to global assembling is computed using accumarray

 b = accumarray(elem2dof(:),bt(:),[Ndof 1]);