AMG TEST II: Different boundary conditions
We consider the linear finite element discretization of Poisson equation on the unstructured mesh with Dirichlet or Neumann boundary conditions.
Contents
load lakemesh
Dirichlet problem
close all;
[N,itStep,time,err] = amgtest(node,elem,1);
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.08, level: 2, coarse grid 434, nnz/Nc 6.21
#dof: 1770, iter: 11, err = 3.5524e-09, time = 0.105 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.59, level: 2, coarse grid 1866, nnz/Nc 6.95
#dof: 7876, iter: 12, err = 2.7907e-09, time = 0.701 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.81, level: 3, coarse grid 1778, nnz/Nc 7.93
#dof: 33081, iter: 15, err = 9.1124e-09, time = 1.92 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.91, level: 4, coarse grid 1573, nnz/Nc 8.39
#dof: 135463, iter: 16, err = 8.9484e-09, time = 5.55 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.95, level: 5, coarse grid 1372, nnz/Nc 8.50
#dof: 548115, iter: 19, err = 7.6833e-09, time = 21.3 s
colHeaders = {'Unknowns','Iterations','Time (sec)','Error'};
makeHtmlTable([N itStep time err],[],[],colHeaders,[],6);
| Unknowns | Iterations | Time (sec) | Error |
| 1770 | 11 | 0.104823 | 3.55242e-09 |
| 7876 | 12 | 0.701491 | 2.79074e-09 |
| 33081 | 15 | 1.92003 | 9.11242e-09 |
| 135463 | 16 | 5.55355 | 8.94844e-09 |
| 548115 | 19 | 21.293 | 7.68333e-09 |
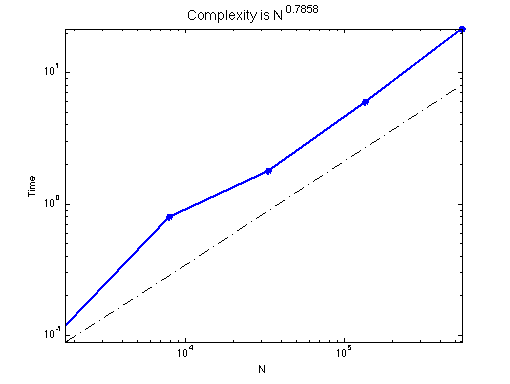
r = showrate(N,time,2);
xlabel('N'); ylabel('Time');
title(['Complexity is N^{' num2str(r) '}'] ,'Fontsize', 14);
Neumann problem
close all;
[N,itStep,time,err] = amgtest(node,elem,0);
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.08, level: 2, coarse grid 428, nnz/Nc 6.20
#dof: 1770, iter: 11, err = 3.4971e-09, time = 0.119 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.59, level: 2, coarse grid 1861, nnz/Nc 6.99
#dof: 7876, iter: 12, err = 4.2550e-09, time = 0.791 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.81, level: 3, coarse grid 1778, nnz/Nc 7.94
#dof: 33081, iter: 15, err = 4.0780e-09, time = 1.77 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.91, level: 4, coarse grid 1594, nnz/Nc 8.35
#dof: 135463, iter: 18, err = 3.1605e-09, time = 5.95 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.95, level: 5, coarse grid 1360, nnz/Nc 8.43
#dof: 548115, iter: 19, err = 9.2185e-09, time = 21.5 s
colHeaders = {'Unknowns','Iterations','Time (sec)','Error'};
makeHtmlTable([N itStep time err],[],[],colHeaders,[],6);
| Unknowns | Iterations | Time (sec) | Error |
| 1770 | 11 | 0.118842 | 3.49711e-09 |
| 7876 | 12 | 0.790716 | 4.255e-09 |
| 33081 | 15 | 1.76985 | 4.07802e-09 |
| 135463 | 18 | 5.94973 | 3.16049e-09 |
| 548115 | 19 | 21.4668 | 9.21849e-09 |
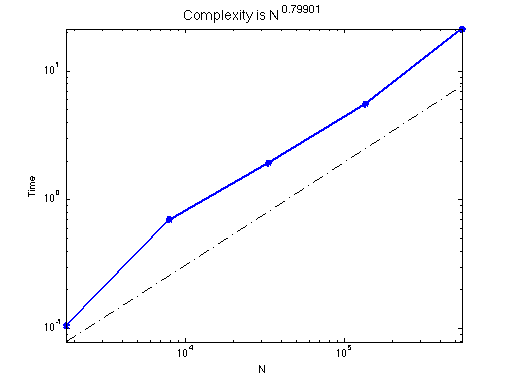
r = showrate(N,time,2);
xlabel('N'); ylabel('Time');
title(['Complexity is N^{' num2str(r) '}'] ,'Fontsize', 14);