AMG TEST III: Robustness to time discretization
We consider the linear finite element discretization of heat equation on the unstructured mesh with Neumann boundary conditions. We test the implicit time discretization with various time stepsizes dt = 1/h^4, 1/h^2, 1/h, 1.
Contents
load lakemesh
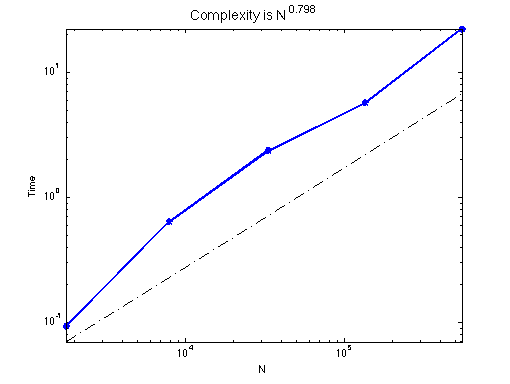
Time step: h^4. Mass matrix will dominate.
close all;
dt = 'h^4';
[N,itStep,time,err] = amgtest(node,elem,2,[],dt);
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.08, level: 2, coarse grid 432, nnz/Nc 6.16
#dof: 1770, iter: 11, err = 4.3648e-09, time = 0.0932 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.59, level: 2, coarse grid 1870, nnz/Nc 6.96
#dof: 7876, iter: 12, err = 7.7321e-09, time = 0.638 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.81, level: 3, coarse grid 1800, nnz/Nc 7.96
#dof: 33081, iter: 16, err = 3.3949e-09, time = 2.37 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.91, level: 4, coarse grid 1581, nnz/Nc 8.40
#dof: 135463, iter: 17, err = 2.6927e-09, time = 5.72 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.95, level: 5, coarse grid 1365, nnz/Nc 8.44
#dof: 548115, iter: 19, err = 5.0467e-09, time = 22.3 s
colHeaders = {'Unknowns','Iterations','Time (sec)','Error'};
makeHtmlTable([N itStep time err],[],[],colHeaders,[],6);
| Unknowns | Iterations | Time (sec) | Error |
| 1770 | 11 | 0.0932378 | 4.36483e-09 |
| 7876 | 12 | 0.638126 | 7.73208e-09 |
| 33081 | 16 | 2.36901 | 3.39492e-09 |
| 135463 | 17 | 5.71547 | 2.69269e-09 |
| 548115 | 19 | 22.2607 | 5.04669e-09 |
r = showrate(N,time,3);
xlabel('N'); ylabel('Time');
title(['Complexity is N^{' num2str(r,3) '}'] ,'Fontsize', 14);
Time step: h^2
close all;
dt = 'h^2';
[N,itStep,time,err] = amgtest(node,elem,2,[],dt);
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.08, level: 2, coarse grid 431, nnz/Nc 6.16
#dof: 1770, iter: 11, err = 4.1611e-09, time = 0.0961 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.59, level: 2, coarse grid 1864, nnz/Nc 6.97
#dof: 7876, iter: 12, err = 3.1055e-09, time = 0.573 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.81, level: 3, coarse grid 1802, nnz/Nc 7.92
#dof: 33081, iter: 16, err = 3.2251e-09, time = 2.03 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.91, level: 4, coarse grid 1607, nnz/Nc 8.47
#dof: 135463, iter: 17, err = 3.2810e-09, time = 5.78 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.95, level: 5, coarse grid 1371, nnz/Nc 8.58
#dof: 548115, iter: 19, err = 5.7017e-09, time = 22.3 s
colHeaders = {'Unknowns','Iterations','Time (sec)','Error'};
makeHtmlTable([N itStep time err],[],[],colHeaders,[],6);
| Unknowns | Iterations | Time (sec) | Error |
| 1770 | 11 | 0.0960589 | 4.16113e-09 |
| 7876 | 12 | 0.573367 | 3.10551e-09 |
| 33081 | 16 | 2.0304 | 3.22508e-09 |
| 135463 | 17 | 5.78185 | 3.28105e-09 |
| 548115 | 19 | 22.3308 | 5.70174e-09 |
r = showrate(N,time,3);
xlabel('N'); ylabel('Time');
title(['Complexity is N^{' num2str(r,3) '}'] ,'Fontsize', 14);

Time step: h
close all;
dt = 'h';
[N,itStep,time,err] = amgtest(node,elem,2,[],dt);
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.08, level: 2, coarse grid 444, nnz/Nc 6.35
#dof: 1770, iter: 11, err = 2.4471e-09, time = 0.109 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.59, level: 2, coarse grid 1858, nnz/Nc 6.92
#dof: 7876, iter: 12, err = 6.5203e-09, time = 0.581 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.81, level: 3, coarse grid 1781, nnz/Nc 7.96
#dof: 33081, iter: 15, err = 4.1690e-09, time = 1.8 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.91, level: 4, coarse grid 1597, nnz/Nc 8.42
#dof: 135463, iter: 17, err = 3.5832e-09, time = 6.61 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.95, level: 5, coarse grid 1412, nnz/Nc 8.49
#dof: 548115, iter: 19, err = 4.1196e-09, time = 52.2 s
colHeaders = {'Unknowns','Iterations','Time (sec)','Error'};
makeHtmlTable([N itStep time err],[],[],colHeaders,[],6);
| Unknowns | Iterations | Time (sec) | Error |
| 1770 | 11 | 0.108834 | 2.4471e-09 |
| 7876 | 12 | 0.581419 | 6.52032e-09 |
| 33081 | 15 | 1.79528 | 4.16904e-09 |
| 135463 | 17 | 6.61341 | 3.58322e-09 |
| 548115 | 19 | 52.1972 | 4.11963e-09 |
r = showrate(N,time,3);
xlabel('N'); ylabel('Time');
title(['Complexity is N^{' num2str(r,3) '}'] ,'Fontsize', 14);

Time step: 1. Like regularized Neumann problem.
close all;
dt = '1';
[N,itStep,time,err] = amgtest(node,elem,2,[],dt);
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.08, level: 2, coarse grid 432, nnz/Nc 6.24
#dof: 1770, iter: 11, err = 3.6669e-09, time = 0.137 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.59, level: 2, coarse grid 1869, nnz/Nc 6.98
#dof: 7876, iter: 12, err = 5.1995e-09, time = 0.567 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.81, level: 3, coarse grid 1779, nnz/Nc 7.93
#dof: 33081, iter: 15, err = 4.0059e-09, time = 1.89 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.91, level: 4, coarse grid 1596, nnz/Nc 8.33
#dof: 135463, iter: 17, err = 3.0391e-09, time = 5.94 s
Multigrid W-cycle Preconditioner with Conjugate Gradient Method
nnz/N: 6.95, level: 5, coarse grid 1350, nnz/Nc 8.44
#dof: 548115, iter: 19, err = 6.0224e-09, time = 21.7 s
colHeaders = {'Unknowns','Iterations','Time (sec)','Error'};
makeHtmlTable([N itStep time err],[],[],colHeaders,[],6);
| Unknowns | Iterations | Time (sec) | Error |
| 1770 | 11 | 0.137216 | 3.66691e-09 |
| 7876 | 12 | 0.567369 | 5.19946e-09 |
| 33081 | 15 | 1.8918 | 4.00592e-09 |
| 135463 | 17 | 5.93713 | 3.03907e-09 |
| 548115 | 19 | 21.7079 | 6.02243e-09 |
r = showrate(N,time,3);
xlabel('N'); ylabel('Time');
title(['Complexity is N^{' num2str(r,3) '}'] ,'Fontsize', 14);




