Coarsening for Algebraic Multigrid: Aggregation

Given a SPD matrix A, we describe an algebraic coarsening of a graph of A based on the concept of strong connectness and aggregation.

Contents

Usage of the function

clear all
help coarsenAMGa

  Parameters

Generate a test matrix

[node,elem] = squaremesh([0,1,0,1],1/32);

[node,elem] = circlemesh(0,0,1,1/11);
% [node,elem] = uniformrefine(node,elem);
% load lakemesh
% load bunny
[A,M] = assemblematrix(node,elem);
% A = M;  % test mass matrix. No coarsening is needed.

 - Min quality 0.8504 - Mean quality 0.9898 - Uniformity 2.94% 

Parameters

theta = 0.025;
N = size(A,1);
N0 = min(sqrt(N),10);       % number of the coarest nodes

Generate strong connectness matrix

D = spdiags(1./sqrt(diag(A)),0,N,N);
Am = D*A*D;  % normalize diagonal of A
[im,jm,sm] = find(Am);
idx = (-sm > theta);   % delete weakly connect off-diagonal and diagonal
As = sparse(im(idx),jm(idx),sm(idx),N,N); % matrix for strong connectness
As = As + speye(N);    % add diagonal
As1 = spones(As);      % graph of As
As2 = triu(As1*As1,1); % edges of the graph corresponding to As^2

Compute degree of vertex

deg = full(transpose(sum(As1))); % number of strongly connected neighbors
if sum(deg>0) < 0.1*sqrt(N)   % too few connected nodes e.g. A is mass matrix
    isC(round(rand(N0,1)*N)) = true; % randomly chose N0 nodes
    return                    % smoother is a good preconditioner
end
idx = (deg>0);
deg(idx) = deg(idx) + 0.1*rand(sum(idx),1); % break the equal degree case

Find an approximate maximal independent set and put to C set

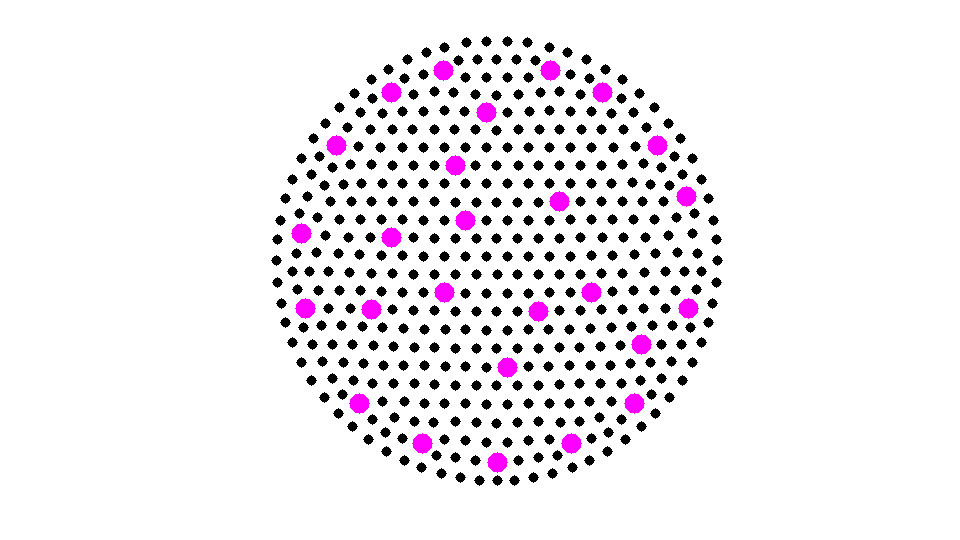
isC = false(N,1);       % C: coarse node
isF = false(N,1);       % F: fine node
isU = true(N,1);
isS = true(N,1);          % S: selected set
isF(deg == 0) = true;   % isolated nodes are added into F set
% debug
close all;
% aggregrate numbering and pointer
aggN = 0;
node2agg = zeros(N,1);
agg2node = zeros(N,1);

set(gcf,'Units','normal');
set(gcf,'Position',[0.5,0.5,0.5,0.5]);
% showmesh(node,elem);
findnode(node,isU,'noindex','Color','k','MarkerSize',32);
axis equal; axis off;
m = 1;
while sum(isC) < N/2 && sum(isS) >N0
    % Mark all undecided nodes
    isS = false(N,1);  % S: selected set, changing in the coarsening
    isS(deg>0) = true;
    S = find(isS);
%     isS(S(2:2:end)) = false;
%     S = S(1:2:end);

    % debug
    fprintf('Coarsening ... \n');

    % Find marked nodes with local maximum degree
%     showagg(node,deg);
    [i,j] = find(As2(S,S));    % i,j and i<j: edges of subgraph S
    idx = deg(S(i)) >= deg(S(j));     % compare degree of vertices
    isS(S(j(idx))) = false;  % remove vertices with smaller degree
    isS(S(i(~idx))) = false;
%     showmesh(node,elem);
    findnode(node,isS,'noindex','Color','m','MarkerSize',60);
    fprintf('Number of chosen points: %6.0u\n',sum(isS));
    snapnow

    % Add new agg
    isC(isS) = true;
    newC = find(isS);
    newAgg = aggN+(1:length(newC));
    aggN = aggN + length(newC);
    node2agg(newC) = newAgg;
    agg2node(newAgg) = newC;
%     showagg(node,node2agg);

    % Remove coarse nodes and neighboring nodes from undecided set
    U = find(isU);
    [i,j] = find(As(isU,newC)); %#ok<*NASGU> use original connectivity
    isF(U(i)) = true;        % neighbor of C nodes are F nodes
    isU = ~(isF | isC);      % U: undecided set
    node2agg(U(i)) = node2agg(newC(j));      % add neighbors into the same aggregrate

    % update degree of U
    deg(newC) = 0;           % remove new selected coarse grid nodes
    deg(U(i)) = 0;           % remove neighbors of new selected coarse grid nodes
    U = find(isU);
    [i,j] = find(As(U,isF)); % find neighbor of fine nodes
    deg(U(i)) = 0;              % remove neighbors of existing agg

    % plot
    figure(1);
%     showmesh(node,elem);
%     findnode(node,isU,'noindex','Color','k','MarkerSize',30);
%     findnode(node,isF,'noindex','Color','y','MarkerSize',48);
%     findnode(node,isC,'noindex','Color','r','MarkerSize',52);
    showagg(node,node2agg,agg2node,As);
    fprintf('Add neighboring nodes into exisitng aggregates. \n');
    snapnow
    m = m + 1;
end
agg2node = agg2node(1:max(node2agg));
fprintf('Apply %2.0u times and Number of Coarse Nodes: %6.0u\n',m,sum(isC));

Coarsening ... 
Number of chosen points:     26

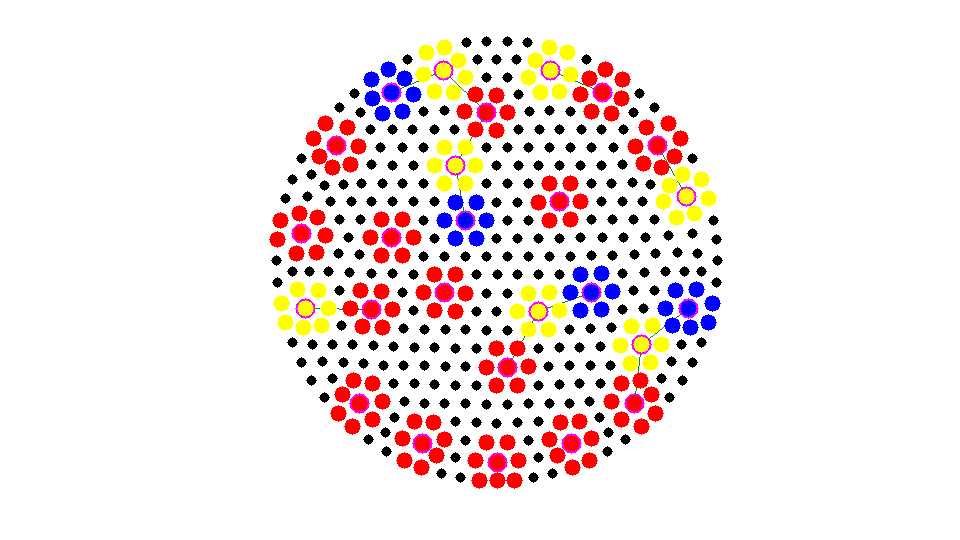
Add neighboring nodes into exisitng aggregates. 

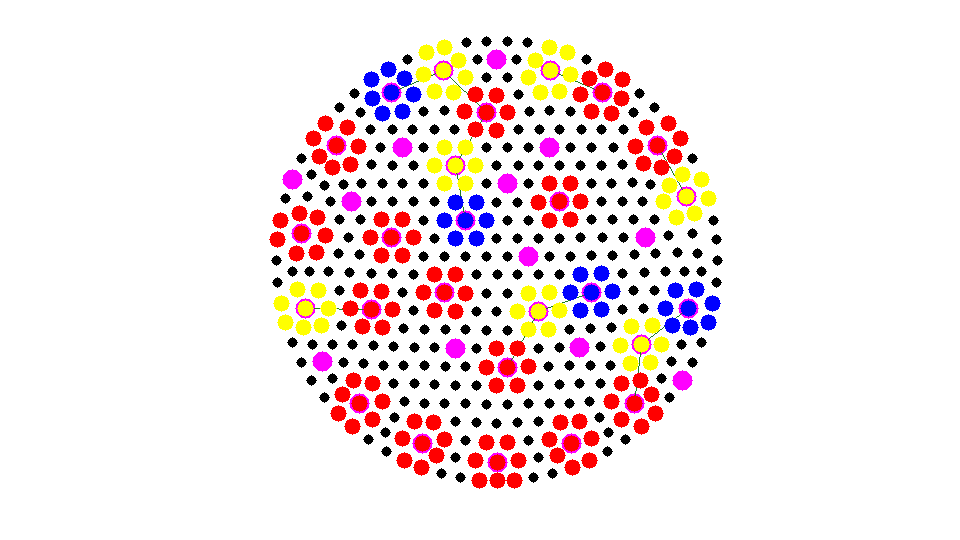
Coarsening ... 
Number of chosen points:     12

Add neighboring nodes into exisitng aggregates. 

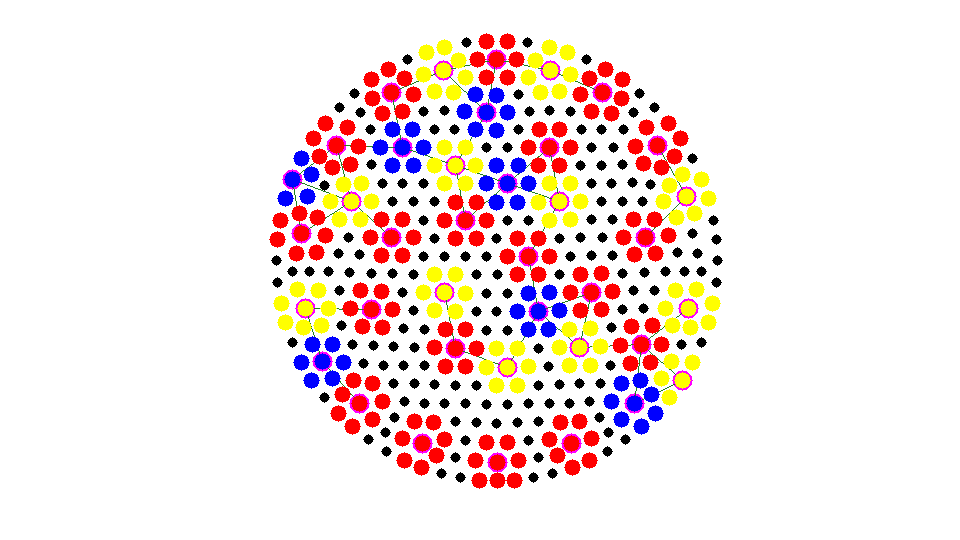
Coarsening ... 
Number of chosen points:      4

Add neighboring nodes into exisitng aggregates. 

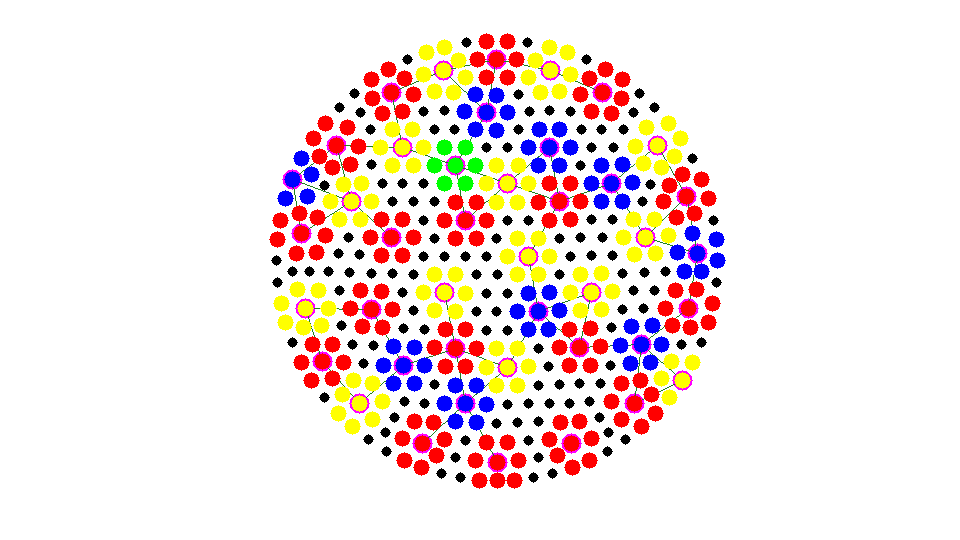
Apply  4 times and Number of Coarse Nodes:     42

Add left vertices to existing aggregate

while any(isU)
    U = find(isU);
    [i,j] = find(As(:,isU)); %#ok<*NASGU> neighboring nodes of U
    % j: undecided vertices; i: neighbor of j
    neighborAgg = node2agg(i); % agg number of neighbors
    idx = (neighborAgg > 0);   % a interior nodes could be left
    [nAgg,neighborAgg] = max(sparse(neighborAgg(idx),j(idx),1));
    % a undecided node could be next to several aggregrates. find the one
    % with maximal neighboring aggregates.
    isbdU = (nAgg > 0);      % find undecided nodes next to
    bdU = U(isbdU);          % the boundary of aggregates
    node2agg(bdU) = neighborAgg(isbdU);
    % remove bdU from U and add to F
    isF(bdU) = true;
    isU(bdU) = false;

%     findnode(node,bdU,'noindex','Color','m');
    showagg(node,node2agg,agg2node,As);
    fprintf('Add left nodes nodes to strongly connected aggregates.\n');
    snapnow
end

Add left nodes nodes to strongly connected aggregates.

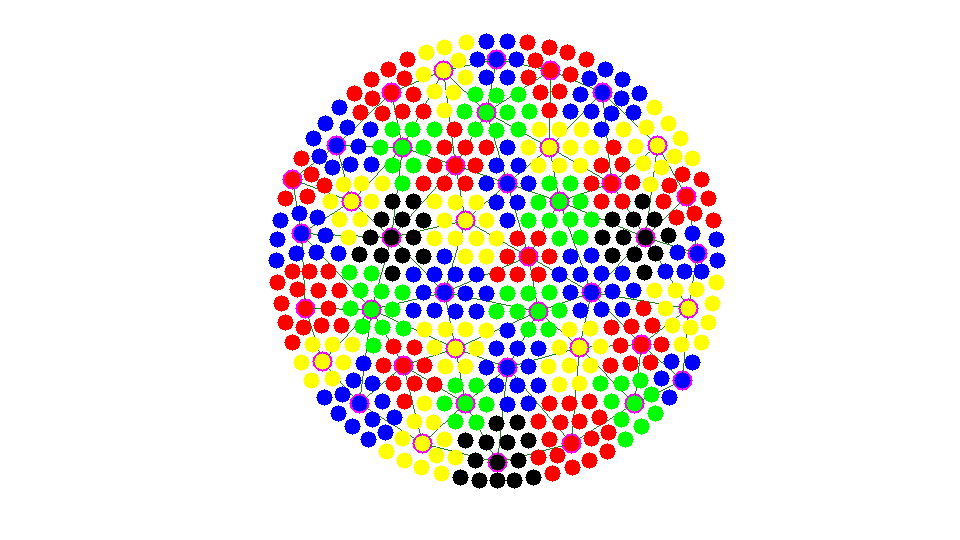
Check the number of nodes in aggregates

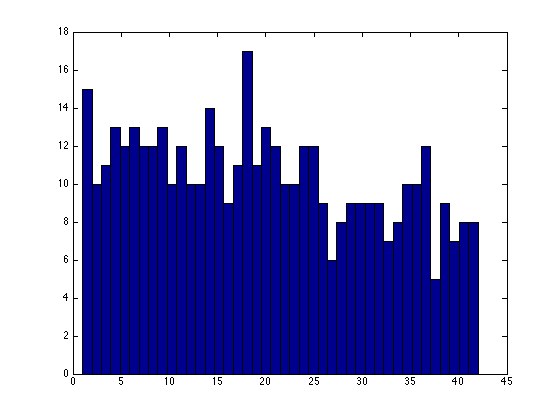
figure;
hist(node2agg,max(node2agg));

Published with MATLAB® 7.14