Coarsening for Algebraic Multigrid
Given a SPD matrix A, we describe an algebraic coarsening of a graph of A based on the concept of strong connectness. The measure of strong connectness is slightly different with the standard definition. The parameter theta is used to define strong connectness and the default value is 0.025.
Contents
Usage of the function
clear all help coarsenAMGc
COARSENAMGC coarsen the graph of A.
isC = coarsenAMGc(A) terturns a logical array to make a set of nodes as
the coarse ndoes based on As, a strong connectness matrix modified from
A. The strong connectness is slightly different with the standard
definition.
[isC,As] = coarsenAMGc(A,theta) accepts the parameter theta to define the
strong connectness. The default setting is theta = 0.025. It also outputs
the strong connectness matrix As which could be used in the constrction
of prolongation and restriction.
Example
load lakemesh
A = assemblematrix(node,elem);
[isC,As] = coarsenAMGc(A);
See also: coarsenAMGrs, interpolationAMGs, amg
Reference page in Help browser
<a href="matlab:ifem coarseAMGdoc">coarsenAMGdoc</a>
Copyright (C) Long Chen. See COPYRIGHT.txt for details.
Generate a test matrix
[node,elem] = squaremesh([0,1,0,1],1/8); % [node,elem] = uniformrefine(node,elem); % load lakemesh [A,M] = assemblematrix(node,elem); % A = M; % test mass matrix. No coarsening is needed.
Parameters
theta = 0.025;
N = size(A,1);
N0 = min(sqrt(N),50); % number of the coarest nodes
Generate strong connectness matrix
D = spdiags(1./sqrt(diag(A)),0,N,N); Am = D*A*D; % normalize diagonal of A [im,jm,sm] = find(Am); idx = (-sm > theta); % delete weakly connect off-diagonal and diagonal As = sparse(im(idx),jm(idx),sm(idx),N,N); % matrix for strong connectness % The diagonal of Am is 1. The negative off-diagonal measures the % diffusivity. The positive off-diagonal is filtered.
Compute degree of vertex
deg = sum(spones(As)); % number of strongly connected neighbors deg = full(deg'); % deg = deg + rand(N,1); % break the equal degree case but deteriorate performance if sum(deg>0) < 0.1*sqrt(N) % too few connected nodes e.g. A is mass matrix isC(round(rand(N0,1)*N)) = true; % randomly chose N0 nodes return % smoother is a good preconditioner end idx = (deg>0); deg(idx) = deg(idx) + 0.1*rand(sum(idx),1); % break the equal degree case
Find an approximate maximal independent set and put to C set
isC = false(N,1); % C: coarse node isF = false(N,1); % F: fine node isU = true(N,1); % S: selected set isF(deg == 0) = true; % isolated nodes are added into F set % debug close all;
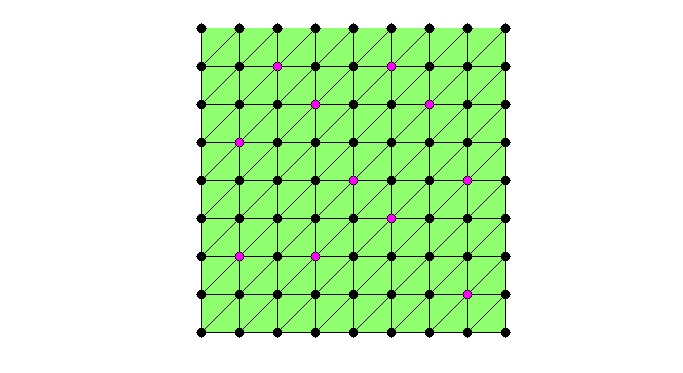
- magneta dots: indepedent nodes in U
- yellow dots: F (fine) nodes
- red dots: C (coarse) nodes
- black dots: U (undecided) nodes
set(gcf,'Units','normal'); set(gcf,'Position',[0.5,0.5,0.5,0.5]); showmesh(node,elem); findnode(node,isU,'noindex','Color','k','MarkerSize',32) while sum(isC) < N/2 && sum(isU) >N0 % Mark all undecided nodes isS = false(N,1); % S: selected set, changing in the coarsening isS(deg>0) = true; S = find(isS); % debug fprintf('Coarsening ... \n'); % Find marked nodes with local maximum degree [i,j] = find(triu(As(S,S),1)); % i,j: index for S idx = deg(S(i)) >= deg(S(j)); % compare degree of vertices isS(S(j(idx))) = false; % remove vertices with smaller degree isS(S(i(~idx))) = false; isC(isS) = true; findnode(node,isS,'noindex','Color','m'); fprintf('Number of chosen points: %6.0u\n',sum(isS)); snapnow % Remove coarse nodes and neighboring nodes from undecided set [i,j] = find(As(:,isC)); %#ok<*NASGU> isF(i) = true; % neighbor of C nodes are F nodes isU = ~(isF | isC); % U: undecided set deg(~isU) = 0; % remove current C and F from the graph % -- No improvement by adding weight to nodes connected to F nodes -- % degFin = sum(spones(As(isF,isU))); % degFin = full(degFin'); % degrer of strong connected with F points % deg(isU) = deg(isU) + degFin; % add weight to nodes connected to F if sum(isU) <= N0 % add small undecided nodes into C nodes isC(isU) = true; isU = []; % to exit the while loop; end % debug showmesh(node,elem); findnode(node,isU,'noindex','Color','k','MarkerSize',32) findnode(node,isC,'noindex','Color','r','MarkerSize',36); findnode(node,isF,'noindex','Color','y','MarkerSize',32) snapnow end fprintf('Number of Coarse Nodes: %6.0u\n',sum(isC));
Coarsening ... Number of chosen points: 11
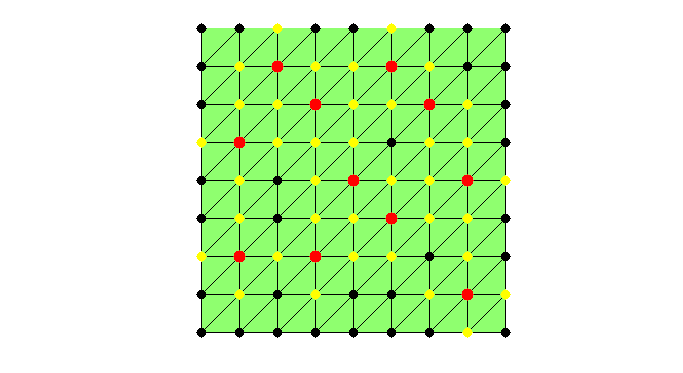
Coarsening ... Number of chosen points: 17
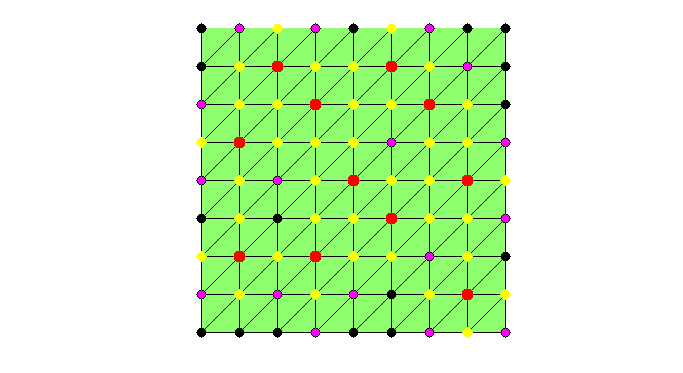
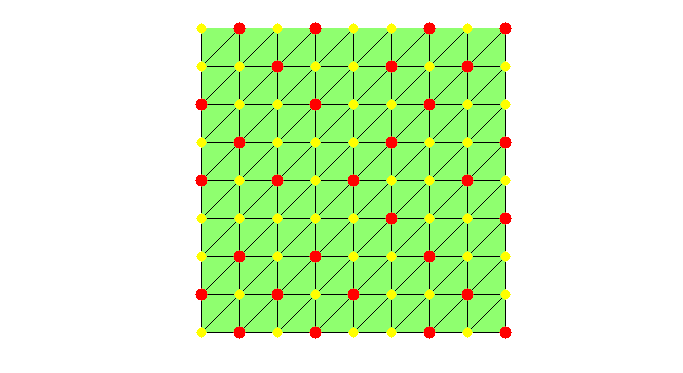
Number of Coarse Nodes: 30
Note that the red nodes are connected in the grid but not connected in the graph of the 5-point stencil.