Contents

function [N,errL2,errH1,erruIuh] = squarePoisson

SQUAREPOISSON Poisson equation in a square domain.

 squarePoisson computes approximations of the Poisson equation in the
 unit square on a sequence of meshes obtained by uniform refinement. It
 plots the approximation error (in L2 norm or H1 norm) vs the number of
 nodes.

See also Poisson, crack

% Copyright (C)  Long Chen. See COPYRIGHT.txt for details.

close all;

Parameters

maxIt = 7; N = zeros(maxIt,1);
errL2 = zeros(maxIt,1); errH1 = zeros(maxIt,1); erruIuh = zeros(maxIt,1);

Generate an initial mesh

node = [0,0; 1,0; 1,1; 0,1];    % nodes
elem = [2,3,1; 4,1,3];          % elements
bdEdge = setboundary(node,elem,'Dirichlet','~(x==0)','Neumann','x==0');
% bdEdge = setboundary(node,elem,'Neumann');
[node,elem,bdEdge] = uniformrefine(node,elem,bdEdge);
% [node,elem,bdEdge] = uniformbisect(node,elem,bdEdge);

Finite Element Method

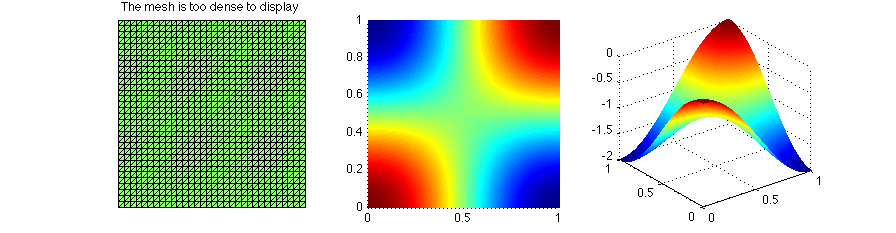
for k = 1:maxIt
    [u,A] = Poisson(node,elem,bdEdge,@f,@g_D,[]);
    figure(1);  showresult(node,elem,u);
    N(k) = size(elem,1);
    % compute error
    errL2(k) = computeL2error(node,elem,@exactu,u);
    errH1(k) = computeH1error(node,elem,@Du,u);
    uI = exactu(node); % nodal interpolation
    erruIuh(k) = sqrt((u-uI)'*A*(u-uI));
    % refine grid
    [node,elem,bdEdge] = uniformrefine(node,elem,bdEdge);
    % [node,elem,bdEdge] = uniformbisect(node,elem,bdEdge);
end

Plot convergence rates

figure(2);
r1 = showrate(N,errH1,2,'-*');
hold on;
r2 = showrate(N,errL2,2,'k-+');
r3 = showrate(N,erruIuh,2,'m-+');
legend('||Du-Du_h||',['N^{' num2str(r1) '}'], ...
       '||u-u_h||',['N^{' num2str(r2) '}'], ...
       '||DuI-Du_h||',['N^{' num2str(r3) '}'], 'LOCATION','Best');

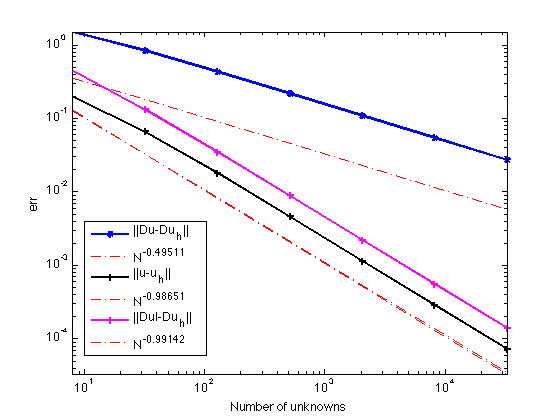
end  % End of SQUAREPOISSON

Data

% load data (right hand side function)
function z = f(p)
x = p(:,1); y = p(:,2);
z = 2*pi^2*cos(pi*x).*cos(pi*y);
end
% exact solution
function z = exactu(p)
x = p(:,1); y = p(:,2);
z = cos(pi*x).*cos(pi*y) - 1;
end
% Dirichlet boundary condition
function z = g_D(p)
z = exactu(p);
end
% Derivative of the exact solution
function z = Du(p)
x = p(:,1); y = p(:,2);
z(:,1) = -pi*sin(pi*x).*cos(pi*y);
z(:,2) = -pi*cos(pi*x).*sin(pi*y);
end

Dof	||u-u_h||	||Du-Du_h||	||DuI-Du_h||
8	0.19792794	1.5035186	0.43962712
32	0.065912866	0.8373829	0.13223755
128	0.017908413	0.43160728	0.034847816
512	0.0045763652	0.21751113	0.0088349807
2048	0.0011504907	0.10897223	0.0022166851
8192	0.0002880262	0.054513305	0.00055467254
32768	7.2031833e-05	0.027260054	0.00013869956

Error table

The optimal rate of convergence of the H1-norm (1st order) and L2-norm (2nd order) is observed. The 2nd order convergent rate between two discrete functions |DuI-Duh| is known as superconvergence.

Published with MATLAB® 7.9