RATE OF CONVERGENCE OF NONCONFORMING LINEAR ELEMENT FOR POISSON EQUATION
This example is to show the rate of convergence of CR non-conforming linear finite element approximation of the Poisson equation on the unit square:
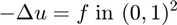
for the following boundary condition:
- Non-empty Dirichlet boundary condition.
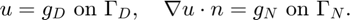
- Pure Neumann boundary condition.
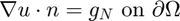 .
. - Robin boundary condition.
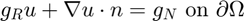
Contents
Setting
[node,elem] = squaremesh([0,1,0,1],0.25); mesh = struct('node',node,'elem',elem); option.L0 = 2; option.maxIt = 4; option.printlevel = 1; option.elemType = 'CR'; option.plotflag = 1;
Non-empty Dirichlet boundary condition.
pde = sincosdata; mesh.bdFlag = setboundary(node,elem,'Dirichlet','~(x==0)','Neumann','x==0'); femPoisson(mesh,pde,option);
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 3136, #nnz: 11040, smoothing: (1,1), iter: 12, err = 2.67e-09, time = 0.026 s
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 12416, #nnz: 44608, smoothing: (1,1), iter: 12, err = 2.62e-09, time = 0.059 s
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 49408, #nnz: 179328, smoothing: (1,1), iter: 12, err = 2.57e-09, time = 0.16 s
#Dof h ||u-u_h|| ||Du-Du_h|| ||DuI-Du_h|| ||uI-u_h||_{max}
800 6.25e-02 1.20226e-03 1.62318e-01 3.64423e-02 1.55737e-03
3136 3.12e-02 3.01351e-04 8.12476e-02 1.81858e-02 3.97664e-04
12416 1.56e-02 7.53872e-05 4.06349e-02 9.08851e-03 1.00099e-04
49408 7.81e-03 1.88499e-05 2.03188e-02 4.54371e-03 2.50778e-05
#Dof Assemble Solve Error Mesh
800 0.00e+00 7.26e-04 1.00e-02 0.00e+00
3136 3.00e-02 2.61e-02 1.00e-02 0.00e+00
12416 8.00e-02 5.87e-02 2.00e-02 3.00e-02
49408 2.30e-01 1.61e-01 8.00e-02 1.20e-01


Pure Neumann boundary condition.
option.plotflag = 0;
pde = sincosNeumanndata;
mesh.bdFlag = setboundary(node,elem,'Neumann');
femPoisson(mesh,pde,option);
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 3136, #nnz: 11325, smoothing: (1,1), iter: 13, err = 4.57e-09, time = 0.016 s
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 12416, #nnz: 45181, smoothing: (1,1), iter: 14, err = 1.91e-09, time = 0.044 s
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 49408, #nnz: 180477, smoothing: (1,1), iter: 14, err = 3.96e-09, time = 0.13 s
#Dof h ||u-u_h|| ||Du-Du_h|| ||DuI-Du_h|| ||uI-u_h||_{max}
800 6.25e-02 5.18787e-03 6.47906e-01 1.49052e-01 6.33147e-03
3136 3.12e-02 1.30793e-03 3.24817e-01 7.31524e-02 1.60037e-03
12416 1.56e-02 3.27672e-04 1.62518e-01 3.64052e-02 4.01216e-04
49408 7.81e-03 8.19609e-05 8.12726e-02 1.81812e-02 1.00375e-04
#Dof Assemble Solve Error Mesh
800 0.00e+00 1.08e-03 0.00e+00 1.00e-02
3136 1.00e-02 1.56e-02 1.00e-02 1.00e-02
12416 4.00e-02 4.41e-02 2.00e-02 2.00e-02
49408 1.40e-01 1.35e-01 8.00e-02 6.00e-02

Pure Robin boundary condition.
pde = sincosRobindata;
mesh.bdFlag = setboundary(node,elem,'Robin');
femPoisson(mesh,pde,option);
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 3136, #nnz: 11328, smoothing: (1,1), iter: 12, err = 1.82e-09, time = 0.011 s
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 12416, #nnz: 45184, smoothing: (1,1), iter: 11, err = 9.89e-09, time = 0.036 s
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 49408, #nnz: 180480, smoothing: (1,1), iter: 12, err = 1.78e-09, time = 0.12 s
#Dof h ||u-u_h|| ||Du-Du_h|| ||DuI-Du_h|| ||uI-u_h||_{max}
800 6.25e-02 5.14818e-03 6.47717e-01 1.48743e-01 6.97115e-03
3136 3.12e-02 1.29781e-03 3.24794e-01 7.31131e-02 1.75333e-03
12416 1.56e-02 3.25127e-04 1.62515e-01 3.64002e-02 4.38609e-04
49408 7.81e-03 8.13241e-05 8.12722e-02 1.81806e-02 1.09622e-04
#Dof Assemble Solve Error Mesh
800 0.00e+00 7.16e-04 0.00e+00 1.00e-02
3136 1.00e-02 1.14e-02 1.00e-02 1.00e-02
12416 4.00e-02 3.55e-02 5.00e-02 2.00e-02
49408 1.30e-01 1.24e-01 9.00e-02 4.00e-02

Conclusion
The optimal rate of convergence of the H1-norm (1st order) and L2-norm (2nd order) is observed. No superconvergence for |DuI-Duh|.
MGCG converges uniformly in all cases.