RATE OF CONVERGENCE OF QUADRATIC ELEMENT FOR POISSON EQUATION
This example is to show the rate of convergence of quadratic finite element approximation of the Poisson equation on the unit square:
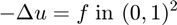
for the following boundary condition:
- Non-empty Dirichlet boundary condition.
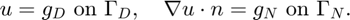
- Pure Neumann boundary condition.
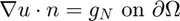 .
. - Robin boundary condition.
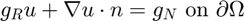
Contents
Setting
[node,elem] = squaremesh([0,1,0,1],0.25); mesh = struct('node',node,'elem',elem); option.L0 = 2; option.maxIt = 4; option.printlevel = 1; option.plotflag = 1; option.elemType = 'P2';
Non-empty Dirichlet boundary condition.
pde = sincosdata; mesh.bdFlag = setboundary(node,elem,'Dirichlet','~(x==0)','Neumann','x==0'); femPoisson(mesh,pde,option);
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 4225, #nnz: 39184, smoothing: (1,1), iter: 11, err = 7.55e-10, time = 0.023 s
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 16641, #nnz: 160272, smoothing: (1,1), iter: 11, err = 7.19e-10, time = 0.077 s
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 66049, #nnz: 648208, smoothing: (1,1), iter: 11, err = 6.86e-10, time = 0.27 s
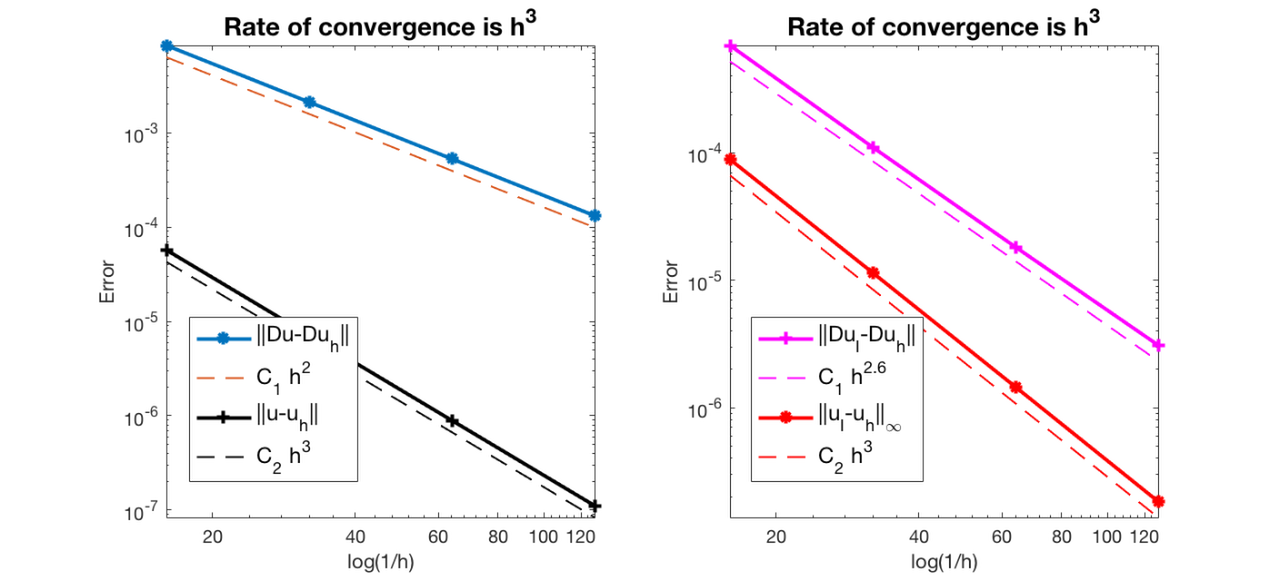
#Dof h ||u-u_h|| ||Du-Du_h|| ||DuI-Du_h|| ||uI-u_h||_{max}
1089 6.25e-02 5.70490e-05 8.40318e-03 6.97560e-04 8.88533e-05
4225 3.12e-02 7.13419e-06 2.10745e-03 1.10743e-04 1.14531e-05
16641 1.56e-02 8.92199e-07 5.27421e-04 1.82456e-05 1.45475e-06
66049 7.81e-03 1.11557e-07 1.31907e-04 3.09580e-06 1.83386e-07
#Dof Assemble Solve Error Mesh
1089 1.00e-02 2.09e-03 1.00e-02 0.00e+00
4225 5.00e-02 2.28e-02 4.00e-02 0.00e+00
16641 1.70e-01 7.72e-02 6.00e-02 3.00e-02
66049 4.50e-01 2.71e-01 2.10e-01 1.40e-01
Pure Neumann boundary condition.
option.plotflag = 0; pde = sincosNeumanndata; % pde = sincosdata; mesh.bdFlag = setboundary(node,elem,'Neumann'); femPoisson(mesh,pde,option);
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 4225, #nnz: 41458, smoothing: (1,1), iter: 13, err = 5.23e-10, time = 0.028 s
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 16641, #nnz: 164850, smoothing: (1,1), iter: 14, err = 2.47e-10, time = 0.076 s
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 66049, #nnz: 657394, smoothing: (1,1), iter: 14, err = 5.84e-10, time = 0.28 s
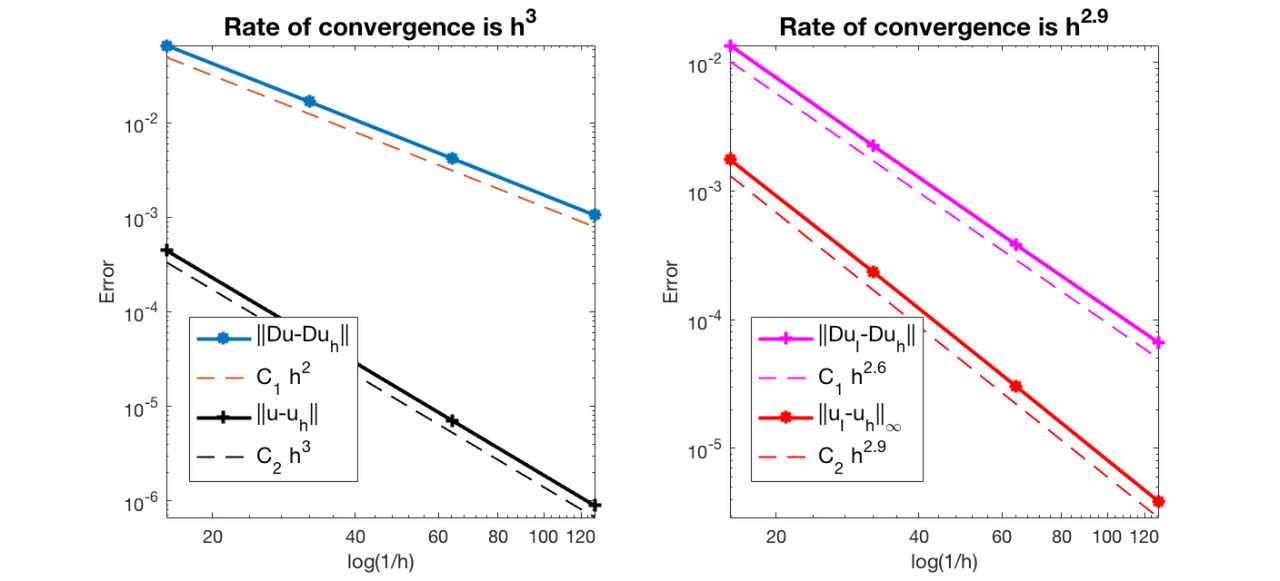
#Dof h ||u-u_h|| ||Du-Du_h|| ||DuI-Du_h|| ||uI-u_h||_{max}
1089 6.25e-02 4.45898e-04 6.57576e-02 1.35282e-02 1.75150e-03
4225 3.12e-02 5.64820e-05 1.67107e-02 2.25947e-03 2.36781e-04
16641 1.56e-02 7.10333e-06 4.20307e-03 3.84722e-04 3.06054e-05
66049 7.81e-03 8.90408e-07 1.05337e-03 6.65670e-05 3.88530e-06
#Dof Assemble Solve Error Mesh
1089 1.00e-02 3.36e-03 1.00e-02 0.00e+00
4225 3.00e-02 2.83e-02 1.00e-02 1.00e-02
16641 1.00e-01 7.56e-02 7.00e-02 2.00e-02
66049 5.00e-01 2.79e-01 1.80e-01 5.00e-02
Pure Robin boundary condition.
option.plotflag = 0;
pde = sincosRobindata;
mesh.bdFlag = setboundary(node,elem,'Robin');
femPoisson(mesh,pde,option);
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 4225, #nnz: 41473, smoothing: (1,1), iter: 11, err = 9.54e-10, time = 0.019 s
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 16641, #nnz: 164865, smoothing: (1,1), iter: 12, err = 1.74e-10, time = 0.063 s
Multigrid V-cycle Preconditioner with Conjugate Gradient Method
#dof: 66049, #nnz: 657409, smoothing: (1,1), iter: 12, err = 1.97e-10, time = 0.28 s
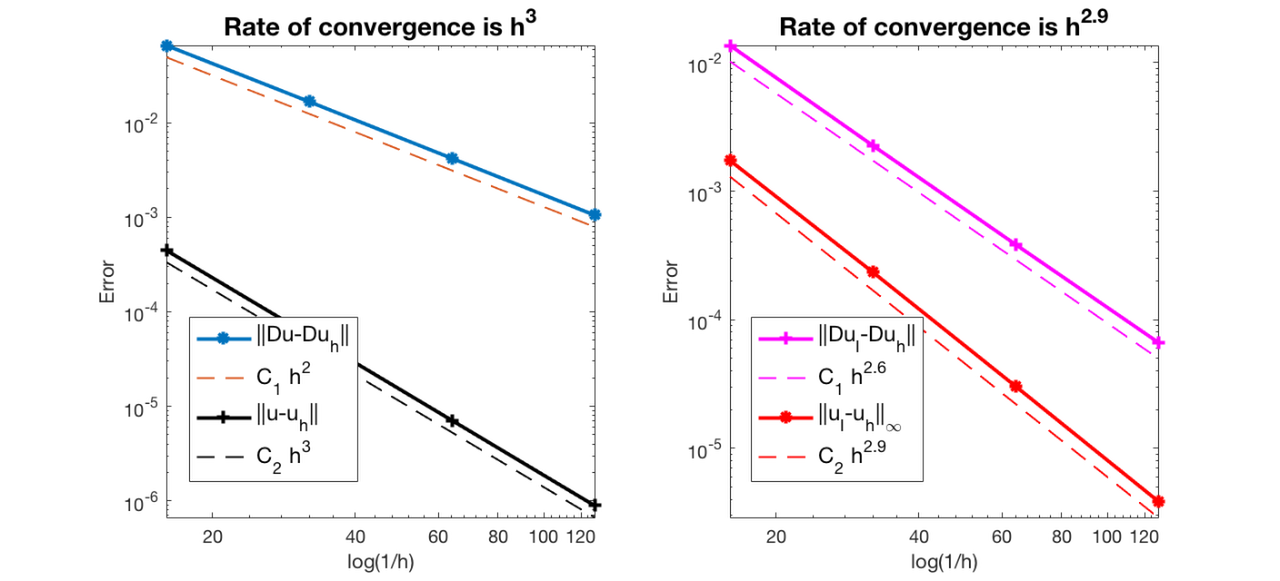
#Dof h ||u-u_h|| ||Du-Du_h|| ||DuI-Du_h|| ||uI-u_h||_{max}
1089 6.25e-02 4.46184e-04 6.57577e-02 1.36110e-02 1.73084e-03
4225 3.12e-02 5.64917e-05 1.67107e-02 2.26778e-03 2.34617e-04
16641 1.56e-02 7.10364e-06 4.20307e-03 3.85477e-04 3.04111e-05
66049 7.81e-03 8.90418e-07 1.05337e-03 6.66341e-05 3.86933e-06
#Dof Assemble Solve Error Mesh
1089 1.00e-02 2.36e-03 1.00e-02 0.00e+00
4225 1.00e-02 1.88e-02 2.00e-02 0.00e+00
16641 9.00e-02 6.31e-02 5.00e-02 1.00e-02
66049 3.10e-01 2.78e-01 2.30e-01 5.00e-02
Conclusion
The optimal rate of convergence of the H1-norm (2nd order) and L2-norm (3rd order) is observed. The order of |DuI-Duh| is 2.5 order and thus superconvergence exists.
MGCG converges uniformly in all cases.