Project: Finite Difference Methods

The purpose of this project is to write a finite difference code for solving the Poisson equation in a rectangular domain using matrix-free or tensor product matrix.

Reference:

Step 1: Generate a uniform grid and evaluate the right hand side
Step 2: Implement A*u
Step 3: Impose boundary conditions
Step 4: Solve linear algebraic systems
Step 5: Convergence

Step 1: Generate a uniform grid and evaluate the right hand side

Use meshgrid or ndgrid to generate a uniform grid of 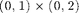$(0,1)\times (0,2)$ for a given mesh size $h$ .

Evaluate f(x,y) at this uniform grid.

Step 2: Implement A*u

Compare the following three ways of computing A*u

Generate a big sparse matrix using the tensor product of 1-D tri-diagonal finite difference matrix and compute A*u using the matrix

Code matrix-free version of A*u

Use the tensor product structure to compute A*u without forming the matrix

Use them to verify the truncation error. That is, choosing the exact solution u and compute the max norm | A*u - f |. Change h and check the order of truncation error.

Step 3: Impose boundary conditions

Dirichlet boundary condition Evaluate the boundary condition at boundary vertices and move to the right hand side.

Neumann boundary condition Change the stencil near the boundary and modify the right hand side.

Step 4: Solve linear algebraic systems

Direct methods: Use the big matrix to solve u = A\f.
Iterative methods: Implement Gauss-Seidel method B(u,f) and iterate

while err > tol
 u = B(u,f);
 err = norm(f-A*u);
end

Step 5: Convergence

Choose a smooth solution and calculate the right hand side f and boundary conditions for the unit square.
Compute the error uI - uh in maximum norm, where uI is the nodal interpolation.
Change mesh size h and check the order of convergence