Project: Linear Finite Element Methods

The purpose of this project is to write a finite element code for solving the Poisson equation in a general polygonal domain using piecewise linear finite elements.

Step 1: Download and Install iFEM
Step 2: Mesh
Step 3: Assembling
Step 4: Right hand side
Step 5: Boundary conditions
Step 6: Convergence

Step 1: Download and Install iFEM

Download iFEM
Unzip the file to where you like
In MATLAB, go to the iFEM folder
Run setpath.m

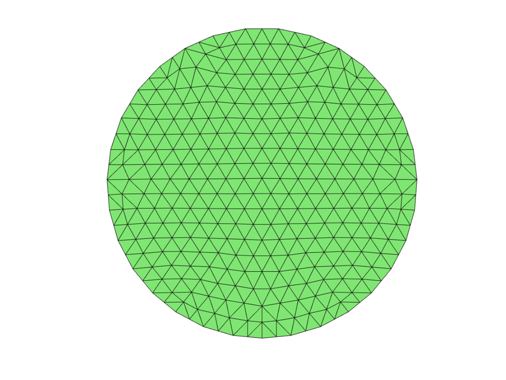
Step 2: Mesh

Generate mesh for square and disk domains

[node,elem] = squaremesh([0,1,0,1],0.25);
showmesh(node,elem);

[node,elem] = circlemesh(0,0,1,0.2);
showmesh(node,elem);

 - Min quality 0.7571 - Mean quality 0.9696 - Uniformity 4.34%

Uniform refine to get a finer mesh

[node,elem] = uniformrefine(node,elem);
showmesh(node,elem);

Step 3: Assembling

Compare three ways of assembling stiffness matrix discussed in Programming of FEM.

   profile on
   tic; assemblingstandard; toc;
   tic; assemblingsparse; toc;
   tic; assembling; toc;
   profile viewer

Compare the computational time for different N (by uniform refinement of the initial mesh).

Step 4: Right hand side

Using three points quadrature (i.e. 3 middle points of a triangle) to compute the right hand side vector.

Step 5: Boundary conditions

Use findboundary.m to get all boundary nodes and edges
Code pure Dirichlet boundary condition
Code pure Neumann boundary condition
(optional) Code pure Robin boundary condition 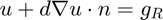$u + d\nabla u\cdot n = g_R$ on the boundary

Step 6: Convergence

Choose a smooth solution, say 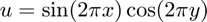$u = \sin(2\pi x)\cos(2\pi y)$ , calculate the right hand side f and boundary conditions for the unit square.
Use your subroutine to get an approximation and use showresult to plot the mesh and the solution.
Use uniformrefine.m to refine the grid and compute a sequence of solutions.
Compute the error in H1 norm and L2 norm using getH1error and getL2error.
Compute the error | |D u_I - D u_h| |, where |u_I | is the nodal interpolation, using the stiffness matrix.
Use showrateh to plot the error and the rate of convergence.

Code your subroutine in a general way such that you can solve the Poisson equation on a different mesh by changing the input arguments. After you get the desireable results for the unit square, try to solve 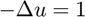$-\Delta u = 1$ with constant Neumann boundary conditions on the unit disk. The exact solution can be found using the polar coordinate.