Project: Transient Navier-Stokes Equations

The purpose of this project is to implement numerical methods for solving time-dependent Navier-Stokes equations in two dimensions.

Contents

Problem setting: Flow past a cylinder

The domain is

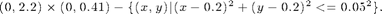
$$ (0,2.2)\times (0,0.41) - \{(x,y) | (x-0.2)^2+(y-0.2)^2 <= 0.05^2\}. $$

The center of the cylinder is slightly off the center of the channel vertically which eventually leads to asymmetry in the flow.

We are solving the Navier-Stokes equation

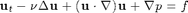
$$ \mathbf u_t -\nu \Delta \mathbf u + (\mathbf u\cdot \nabla) \mathbf u + \nabla p = f $$

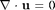
$$ \nabla \cdot \mathbf u = 0 $$

The time-dependent inflow boundary condition on the left is

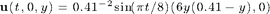
$$ \mathbf u(t,0,y) = 0.41^{-2}\sin(\pi t/8)(6y(0.41-y), 0) $$

The outflow boundary condition on the right 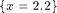$$ \{x= 2.2\} $$ is

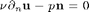
$$ \nu \partial_n \mathbf u - p \mathbf n = 0 $$

On the other part of the boundary, no-slip boundary condition 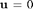$$ \mathbf u = 0 $$ is imposed.

The initial condition is zero 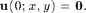$$ \mathbf u(0; x,y) = \mathbf 0. $$

The body force is zero too $$ \mathbf f = \mathbf 0. $$

We choose 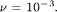$$ \nu = 10^{-3}. $$ Since the maximum velocity is one and the diameter of the cylinder is 0.1, the Reynolds number of the flow is 100.

Step 1: Mesh

Download the mesh flowpastcylindermesh.mat and load it in Matlab.

load flowpastcylindermesh
showmesh(node,elem); axis on; axis tight;
set(gcf,'Units','normal');
set(gcf,'Position',[0.125,0.125,0.35,0.2]);

When uniform refine this coarse grid, you need to project the circular part back to the circle.

Step 2: FEM for convection-diffusion-reaction equations

Choose either non-conforming P1 - P0 or iso P2-P0 elements.

Besides the matrix for Laplacian and divergence operator, you need to compute one more matrix for the convection term 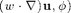$$ (w\cdot \nabla)\mathbf u, \mathbf \phi) $$ and the mass matrix for the reaction term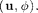 $$ ( \mathbf u, \mathbf \phi). $$

The mass matrix for non-conforming P1 is diagonal. For P1 element, use mass lumping to compute a diagonal mass matrix.

For convection term, first write out component-wise weakformulation and compute the element-wise entry and finally assemble the matrix. Note that the derivative of a linear basis is constant which can be factor out the integral and one-point quadrature is good enough.

Test your code for a scalar convection-diffusion-reaction equation

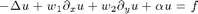
$$ - \Delta u + w_1 \partial _x u + w_2 \partial _y u + \alpha u = f $$

by choosing a smooth function and moderate convection coefficient.

Step 3: Time Discretization and Nonlinear Iteration for N-S equations

Step 4: GMRES method for solving the linearied problem

Suppose the linear saddle point system system is [ F B'; B 0 ]. Use the block-triangular preconditioner [F B'; 0 -BF^{-1}B']^{-1} and GMRES to solve the linear system to the tolerence 1e-6.

The inverse of the Schur complement is approximated by the least-square commutator

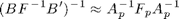
$$ (BF^{-1}B')^{-1} \approx A_p^{-1}F_pA_p^{-1} $$

where

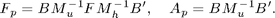
$$ F_p = BM_u^{-1}FM_h^{-1}B', \quad A_p = BM_u^{-1}B'. $$

The Poisson solver 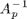$$ A_p^{-1} $$ can be replaced by the direct solver or one V-cycle.

Step 5: Evaluation of the Computational Results


Published with MATLAB® 7.14