Project: Finite Element for Stokes Equations

The purpose of this project is to implement simple and popular finite element methods for solving Stokes equations in two dimensions.

Contents

Part I: Finite Element Methods: isoP2-P0 element

Given a triangulation (node,elem), the velocity space is the linear finite element space on the uniform refinement of (node,elem) and the pressure is piecewise constant space on the current mesh.

Step 1: Data Structure

Given mesh will be refered as a coarse grid

[node,elem] = squaremesh([-1,1,-1,1],0.25);
NTc = size(elem,1);

% Uniform refinement to a fine grid
[node,elem] = uniformrefine(node,elem);

In the uniformrefine, the new elements are added in such an order that triangles (t, NTc + t, 2*NTc + t, 3*NTc + t) are refined from the same parent, where NTc is the number of triangles in the coarse grid.

Step 2: Form matrices and right hand side for Laplacian

Call your code for linear finite element methods. You can merge two copies of Laplacian using blkdiag.

Step 3: Form matrices for divergence operator

Compute 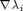on the fine grid

[Dlambda,area] = gradbasis(node,elem);

Assemble sparse matrices for divergence operator on the fine grid by computing .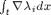

Merge four terms in the above matrix to compute the divergence operator on the coarse grid .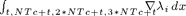

Step 4: Modify equations to include boundary conditions

Modify the right hand side to include Dirichlet or Neumann boundary conditions. It is the same as the Poisson equation. Just repeat for each component. For non-homogenous Dirichlet boundary condition, you need to modify the continunity equation too. Recoard freeDof.

Step 5: Solve the linear system

Form a big matrix bigA = [A B'; B sparse(Np,Np)] and use the direct solver to solve bigA(bigFreeDof,bigFreeDof)\bigF(bigFreeDof)

Since the pressure is unique up to a constant, you need to eliminate the constant kernel by not including one component of pressure vector in the bigFreeDof. After you get the solution, you need to modify p such that its weighted mean value is zero.

Part II: Finite Element Methods: nonforming P1-P0 element

Step 1: Data Structure

Since the unknowns are associated to edges, you need to generate edges and more importantly the indices map from a triangle to global indices of its three edges. The edges are labled such that the i-th edge is opposite to the i-th vertex for i=1,2,3.

[elem2edge,edge] = dofedge(elem);

Step 2: Form matrices and right hand side

Figure out the basis of CR element. Hint: use barycenteric coordinates it can be writeen as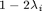

Call your code for linear finite element methods in Part I with the correct scaling.

Compute the righ hand side using three middle point rule. It is even simplier than linear element case.

Step 3: Modify equations to include boundary conditions

Similar as in the linear element case. Just be careful on the Dirichlet boundary condition, you need to evaluate g_D at middle points of boundary edges.

To find out the boundary edges, use

s = accumarray(elem2edge(:), 1, [size(edge,1) 1]);

Then idx = (s==1) is the index of boundary edges and (s==2) is interiori (free) edges.

Step 4: Solve the linear system

Same as the first Part.

Part III: Test Example

We use a simple model of colliding flow with analytic solutions to test the code. The domain is [-1,1]^2 and the analytic solution is:

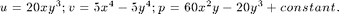
Compute the data f and Dirichlet boundary condition g_D and solve Stokes equation on the unit square using methods in Part I,II,II and check the rate of convergence.

Published with MATLAB® 7.14