Project: Wave Equation

In this project we will code finite element or finite difference methods for solving the wave equation.

Contents

Wave Equation

$$ u_{tt} - \Delta u = f, \quad x\in \Omega, t\in (0,T], $$

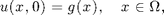
$$ u(x,0) = g(x), \quad x\in \Omega, $$

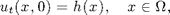
$$ u_{t}(x,0) = h(x), \quad x\in \Omega, $$

$$ u = u_D, \quad x\in \partial \Omega, t\in (0,T].$$

Leapfrog Method

It is a second order explicit method for solving the wave equation.

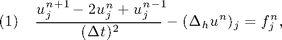
$$ (1) \quad \frac{u_j^{n+1}-2u_j^n+ u_{j}^{n-1}}{(\Delta t)^2} - (\Delta _h u^n)_j = f^n_j,$$

where 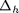$$ \Delta _h $$ is a discretization of 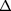$$ \Delta $$ operator using finite difference or finite element method. You are free to chose the one you like. When using finite element methods, you can use mass lumping and multiply the inverse of mass matrix to get a formulation like (1).

Choose 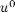$u^0$ by the nodal interpolation, i.e., 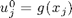$u^0_j=g(x_j)$. To get 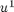$u^1$, we introduce the ghost point 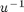$u^{-1}$ and discretizate the initial velocity using the central difference:

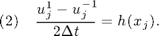
$$ (2) \quad \frac{u^1_j-u^{-1}_j}{2\Delta t} = h(x_j). $$

We use (2) and (1) at $n =0$ to eliminate the ghost point and obtain a formula for $u^1$.

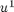Test Example

We choose the domain as 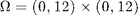$\Omega = (0,12)\times (0,12)$ and the source term as

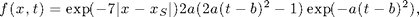$$ f(x,t) = \exp(-7|x-x_S|) 2a(2a(t-b)^2-1)\exp(-a(t-b)^2), $$ where

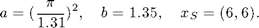
$$ a = (\frac{\pi}{1.31})^2, \quad b=1.35, \quad x_S = (6,6). $$

The boundary and initial conditions

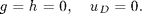
$$ g = h = 0, \quad u_D = 0. $$

Output

Check the rate of convergence is second order in both time and space.

Hint When the exact solution is not known, use the double grid principle to estimate the errors. That is, compute the difference between solutions of two consective meshes (the finer one is the uniform refinemen of the coarser one).

When you verify the rate of h, choose dt small enough. Similarly fix a small h and vary dt to verify the rate in time.

Read the example in getframe documentation on how to creat a movie in matlab.

Run your code and record the movie of the evolution of the function.


Published with MATLAB® 7.14