
|
|
|
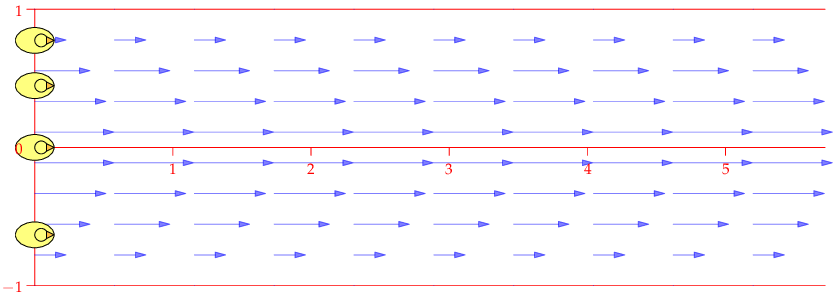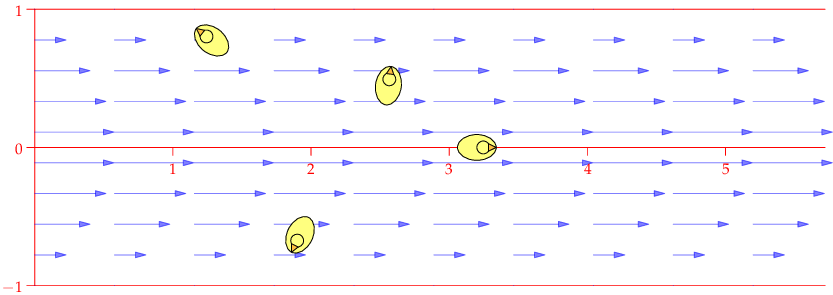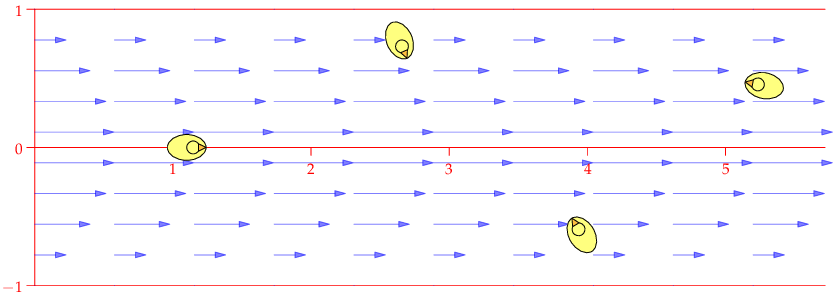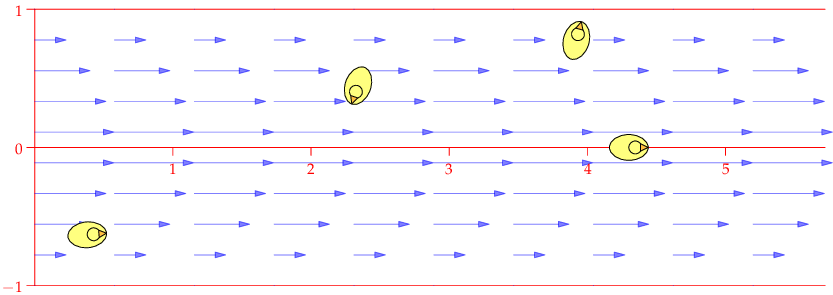
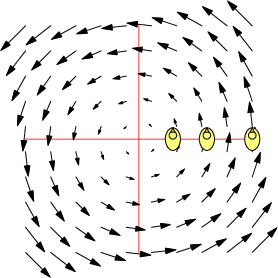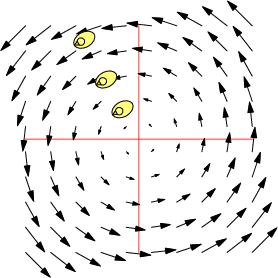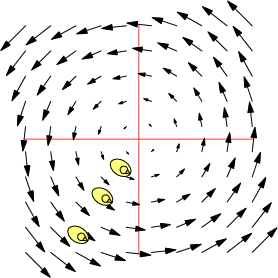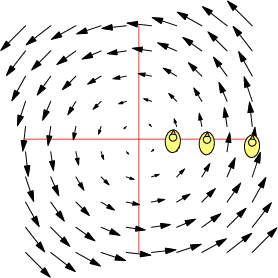
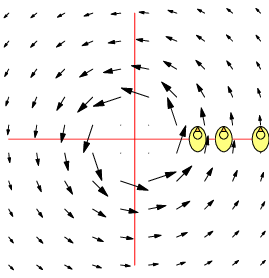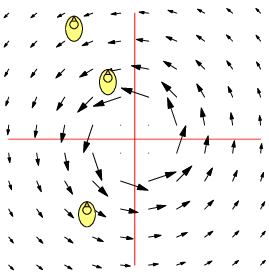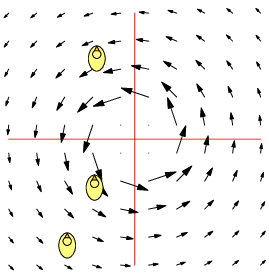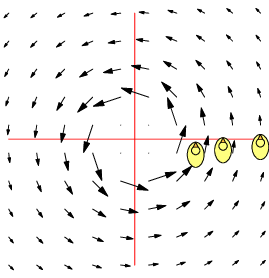
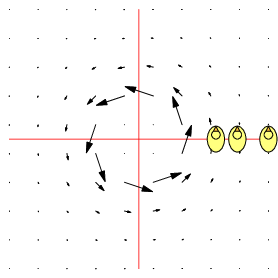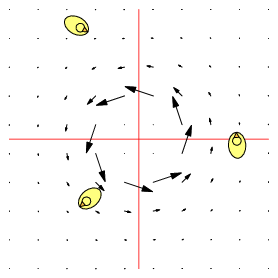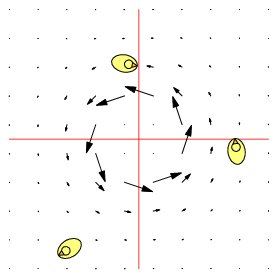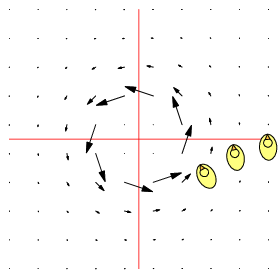
| $\mathbf F=\binom{-y}{x},\quad \nabla\times\mathbf F=2\,\mathbf k$ | $\mathbf F=\frac 1{x^2+y^2}\binom{-y}{x},\quad \nabla\times\mathbf F=\mathbf 0$ | $\mathbf F=\frac 1{(x^2+y^2)^2}\binom{-y}{x},\quad \nabla\times\mathbf F=-\frac 2{(x^2+y^2)^2}\mathbf k$ |
| Counter-clockwise local and global rotation 1 rad/s | Counter-clockwise global rotation. No local rotation | Counter-clockwise global rotation. Clockwise local rotation |