NE2 Quadratic Edge Element (first family) in 3D

Contents

Local Bases

The first 12 bases are associated to edges. We order the local bases as

1- 6: 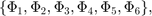$\{\Phi_1, \Phi_2, \Phi_3, \Phi_4, \Phi_5, \Phi_6\},$

7- 12: 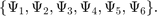$\{\Psi_1, \Psi_2, \Psi_3, \Psi_4, \Psi_5, \Psi_6\}.$

NE0 Lowest order edge element NE1 Linear edge element

Suppose 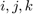$i,j,k$ are the vertices of the 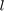$l$-th face and 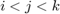$i<j<k$. The two basis associated to this face are

$$ \chi_l^1 = \lambda_j\phi _{ik} = \lambda_j(\lambda_i\nabla\lambda_k - \lambda_k\nabla\lambda_i),\quad \chi_l^2 = \lambda_k\phi _{ij} = \lambda_k(\lambda_i\nabla\lambda_j - \lambda_j\nabla\lambda_i).$$

Inside one tetrahedron, the 8 bases functions assocaited to the four local faces [2 3 4; 1 3 4; 1 2 4; 1 2 3] are:

$$ \chi_1^1 = \lambda_3\phi _{24} = \lambda_3(\lambda_2\nabla\lambda_4 - \lambda_4\nabla\lambda_2),\quad \chi_1^2 = \lambda_4\phi _{23} = \lambda_4(\lambda_2\nabla\lambda_3 - \lambda_3\nabla\lambda_2).$$

$$ \chi_2^1 = \lambda_3\phi _{14} = \lambda_3(\lambda_1\nabla\lambda_4 - \lambda_4\nabla\lambda_1),\quad \chi_2^2 = \lambda_4\phi _{13} = \lambda_4(\lambda_1\nabla\lambda_3 - \lambda_3\nabla\lambda_1).$$

$$ \chi_3^1 = \lambda_2\phi _{14} = \lambda_2(\lambda_1\nabla\lambda_4 - \lambda_4\nabla\lambda_1),\quad \chi_3^2 = \lambda_4\phi _{12} = \lambda_4(\lambda_1\nabla\lambda_2 - \lambda_2\nabla\lambda_1).$$

$$ \chi_4^1 = \lambda_2\phi _{13} = \lambda_2(\lambda_1\nabla\lambda_3 - \lambda_3\nabla\lambda_1),\quad \chi_4^2 = \lambda_3\phi _{12} = \lambda_3(\lambda_1\nabla\lambda_2 - \lambda_2\nabla\lambda_1).$$

Reference: See page 12, Table 9.2. Arnold, Douglas N. and Falk, Richard S. and Winther, Ragnar. Geometric decompositions and local bases for spaces of finite element differential forms. Comput. Methods Appl. Mech. Engrg. 198():1660--1672, 2009.

Locally, we order the local bases in the following way:

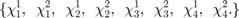
$$\{\chi_1^1,~\,\chi_1^2,~\,\chi_2^1,~\,\chi_2^2,~\,\chi_3^1,~\,\chi_3^2, ~\,\chi_4^1,~\,\chi_4^2.\}$$

and rewrite the local bases as:

13- 20: 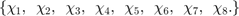$\{\chi_1,~\,\chi_2,~\,\chi_3,~\,\chi_4,~\,\chi_5,~\,\chi_6,~\, \chi_7,~\,\chi_8.\}$

Data Structure

[node,elem] = cubemesh([0,1,0,1,0,1],1);

Locally we construct locBasesIdx to record the local index used in the bases.

locEdge = [1 2; 1 3; 1 4; 2 3; 2 4; 3 4];
locFace = [2 3 4; 1 3 4; 1 2 4; 1 2 3];
locBasesIdx = [1 2 0; 1 3 0; 1 4 0; 2 3 0; 2 4 0; 3 4 0; ... % phi
               1 2 0; 1 3 0; 1 4 0; 2 3 0; 2 4 0; 3 4 0; ... % psi
               3 2 4; 3 1 4; 2 1 4; 2 1 3; ...
               4 2 3; 4 1 3; 4 1 2; 3 1 2]; % chi

For example, for basis 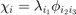$\chi_i =\lambda_{i_1}\phi _{i_2i_3}$ for $i=4$, we can get i1,i2,i3 by:

i = 4+12;
i1 = locBasesIdx(i,1); i2 = locBasesIdx(i,2); i3 = locBasesIdx(i,3);

In addition to the edge structure, we need face and the corresponding pointers.

[elem2edge,edge] = dof3edge(elem);
[elem2face,face] = dof3face(elem);

Furthermore we need pointer from face to edge.

face2edge = zeros(size(face,1),3,'int32');
% face is given by auxtructure3 and is sorted according to global indices.
% locFace = [2 3 4; 1 3 4; 1 2 4; 1 2 3];
% face2edge is used to compute uI. So it is consistent with the local index
% system in edgeinterpolate2, i.e., if face is (i,j,k) with i<j<k, then the
% three edges are [i j], [i k], [j k].
face2edge(elem2face(:,1),:) = elem2edge(:,[4 5 6]);
face2edge(elem2face(:,2),:) = elem2edge(:,[2 3 6]);
face2edge(elem2face(:,3),:) = elem2edge(:,[1 3 5]);
face2edge(elem2face(:,4),:) = elem2edge(:,[1 2 4]);


Published with MATLAB® R2014b