RT0 Lowest Order Edge Element in 2D

We explain degree of freedoms and basis functions for Raviart-Thomas edge element on triangles. The dofs and basis depends on the orientation of the mesh. Read Simplicial complex in two dimensions for the discussion of indexing, ordering and orientation.

Contents

Local bases of RT0 element

Suppose 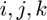$i,j,k$ are the vertices of the 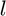$l$-th face. The basis is

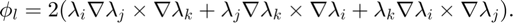
$$ \phi_l = 2(\lambda_i\nabla \lambda_j \times \nabla\lambda_k + \lambda_j\nabla \lambda_k \times \nabla\lambda_i + \lambda_k\nabla \lambda_i \times \nabla\lambda_j).$$

Inside one tetrahedron, the 4 basis functions corresponding to 4 local faces [2 3 4; 1 4 3; 1 2 4; 1 3 2] are:

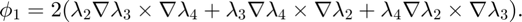
$$ \phi_1 = 2(\lambda_2\nabla \lambda_3 \times \nabla\lambda_4 + \lambda_3\nabla \lambda_4 \times \nabla\lambda_2 + \lambda_4\nabla \lambda_2 \times \nabla\lambda_3).$$

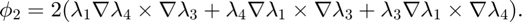
$$ \phi_2 = 2(\lambda_1\nabla \lambda_4 \times \nabla\lambda_3 + \lambda_4\nabla \lambda_1 \times \nabla\lambda_3 + \lambda_3\nabla \lambda_1 \times \nabla\lambda_4).$$

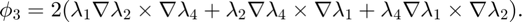
$$ \phi_3 = 2(\lambda_1\nabla \lambda_2 \times \nabla\lambda_4 + \lambda_2\nabla \lambda_4 \times \nabla\lambda_1 + \lambda_4\nabla \lambda_1 \times \nabla\lambda_2).$$

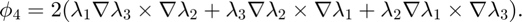
$$ \phi_4 = 2(\lambda_1\nabla \lambda_3 \times \nabla\lambda_2 + \lambda_3\nabla \lambda_2 \times \nabla\lambda_1 + \lambda_2\nabla \lambda_1 \times \nabla\lambda_3).$$

The dual basis is the line integral over an orientated face

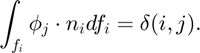
$$\int_{f_i} \phi_j \cdot n_i df_i = \delta(i,j).$$

Data Structure

We use ascend ordering system. [elem,bdFlag] = sortelem3(elem,bdFlag); [elem2dof,face] = dof3face(elem); NT = size(elem,1); NF = size(face,1); localFace = [2 3 4; 1 3 4; 1 2 4; 1 2 3];

Matrix for divergence operator

Mass Matrix

We use the integral formula

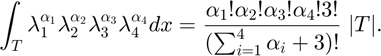
$$ \int_T \lambda_1^{\alpha_1}\lambda_2^{\alpha_2}\lambda_3^{\alpha_3}\lambda_4^{\alpha_4} dx = \frac{\alpha_1!\alpha_2!\alpha_3!\alpha_4!3!}{(\sum _{i=1}^4\alpha_i + 3)!}\;|T|.$$

see Poisson3RT0.m


Published with MATLAB® R2015b