RT0 Lowest Order Edge Element in 2D

We explain degree of freedoms and basis functions for Raviart-Thomas edge element on triangles. The dofs and basis depends on the orientation of the mesh. Read Simplicial complex in two dimensions for the discussion of indexing, ordering and orientation.

Contents

Local bases of RT0 element

Suppose [i,j] is the k-th edge. The two dimensional curl is a rotated graident defined as 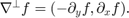$\nabla^{\bot} f = (-\partial_y f, \partial _x f).$ The basis of this edge along with its divergence are given by

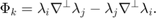
$$ \Phi_k = \lambda_i \nabla^{\bot} \lambda_j - \lambda_j \nabla^{\bot} \lambda_i. $$

Inside one triangular, the 3 bases corresponding to 3 local edges [2 3; 1 3; 1 2] are:

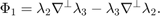
$$ \Phi_1 = \lambda_2 \nabla^{\bot} \lambda_3 - \lambda_3 \nabla^{\bot} \lambda_2. $$

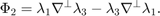
$$ \Phi_2 = \lambda_1 \nabla^{\bot} \lambda_3 - \lambda_3 \nabla^{\bot} \lambda_1. $$

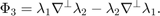
$$ \Phi_3 = \lambda_1 \nabla^{\bot} \lambda_2 - \lambda_2 \nabla^{\bot} \lambda_1. $$

The dual basis is the line integral over an orientated edge

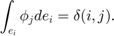
$$\int_{e_i} \phi_j de_i = \delta(i,j).$$

Data Structure

We use ascend ordering system. Note that the signed area of some triangles could be negative.

[node,elem] = squaremesh([0 1 0 1], 0.5);
bdFlag = setboundary(node,elem,'Dirichlet');
[elem,bdFlag] = sortelem(elem,bdFlag);
showmesh(node,elem);
findnode(node);
findelem(node,elem);
% Three local edges are |locEdge = [2 3; 1 3; 1 2]|. The pointer from the
% local to global index can be constructured by
[elem2dof,edge] = dofedge(elem);
findedge(node,edge,'all','vec');

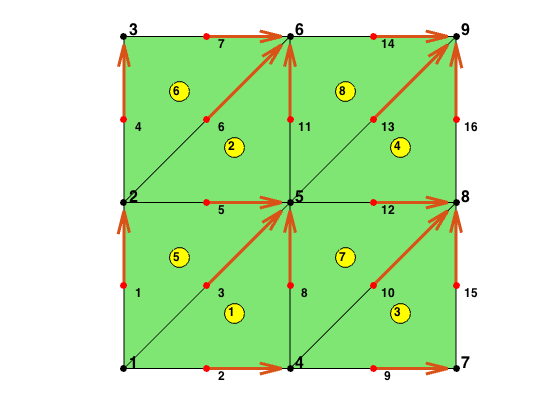
display(elem);
display(elem2dof);

elem =

     1     4     5
     2     5     6
     4     7     8
     5     8     9
     1     2     5
     2     3     6
     4     5     8
     5     6     9


elem2dof =

           8           3           2
          11           6           5
          15          10           9
          16          13          12
           5           3           1
           7           6           4
          12          10           8
          14          13          11

The global and local orientation of edges are induced from the ascend ordering of vertices. Thanks to the ascend ordering, the local and global orientation are consistent.

However the ordering orientation is not consistent with the induced orientation. The second edge would be [3 1] for the consistent orientation. So [1 -1 1] is used in the construction of div operator.

Matrix for divergence operator

For triangle t, the basis for the constant function space is p = 1, the characteristic function. So in the computation of divergence operator, elemSign should be used. In the output of gradbasis, -Dlambda is always the outwards normal direction. The signed area could be negative but in the ouput, area is the absolute value (for the easy of integration on elements). Thus elemSign is used to record elements with negative area.

[Dlambda,area,elemSign] = gradbasis(node,elem);
B = icdmat(double(elem2dof),elemSign*[1 -1 1]);
display(full(B))

ans =

  Columns 1 through 13

     0     1    -1     0     0     0     0     1     0     0     0     0     0
     0     0     0     0     1    -1     0     0     0     0     1     0     0
     0     0     0     0     0     0     0     0     1    -1     0     0     0
     0     0     0     0     0     0     0     0     0     0     0     1    -1
    -1     0     1     0    -1     0     0     0     0     0     0     0     0
     0     0     0    -1     0     1    -1     0     0     0     0     0     0
     0     0     0     0     0     0     0    -1     0     1     0    -1     0
     0     0     0     0     0     0     0     0     0     0    -1     0     1

  Columns 14 through 16

     0     0     0
     0     0     0
     0     1     0
     0     0     1
     0     0     0
     0     0     0
     0     0     0
    -1     0     0


Published with MATLAB® R2014b