Project: Multigrid Methods

In this project we will learn three ways of implementating multigrid methods: from matrix-free version to matrix-only version depending on how much information on the grid and PDE is provided.

Multigrid on Uniform Grids for Poisson Equations
Step 1 Smoother
Step 2 Two-Grid method
Step 3 V-cycle Multi-grid method
Multigrid on Hierarchical Grids
Step 1 Hierarchical Meshes
Step 2 Transfer Operator and Smoothers
Step 3 V-cycle Multigrid
Algebraic Multigrid Method
Step 1 Matrix
Step 2 Coarsening
Step 3 Transfer Operator and Smoothers
Step 4 V-cycle Multigrid used with PCG

Multigrid on Uniform Grids for Poisson Equations

We consider linear finite element or equivalently 5-point stencil discretization of the Poisson equation on a uniform grid of [0,1]^2 with size h. For simplicity, we assume h = 1/2^L and zero Dirichlet bounary condition.

set(gcf,'Units','normal'); set(gcf,'Position',[0,0,0.4,0.3]);
[node,elem] = squarequadmesh([0,1,0,1],0.25);
subplot(1,2,1); showmesh(node,elem);
[node,elem] = uniformrefinequad(node,elem);
subplot(1,2,2); showmesh(node,elem);

Step 1 Smoother

Code weighted Jacobi and Gauss-Seidel smoother; see projectFDM.html

Check the convergence of Gauss-Seidel smoother by solving 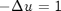$-\Delta u = 1$ in (0,1)^2 with zero Dirichlet boundary condition. Plot the error in suitable norm vs iteration for h = 1/64.

Change h from 1/4 to 1/128 and compare the iterations to drive the relative error in a suitable norm below the discretiztion error h^2.

Choose a random initial guess. Plot the error function on the grid for the first 3 steps.

(Optional) Code the red-black Gauss-Seidel.

Step 2 Two-Grid method

Figure out the index map between fine grid with size h and coarse grid with size 2h. For example, (i,j) in coarse grid is (2*i-1,2*j-1) in the fine grid.

Code the bilinear prolongation and restriction using the index map. Be carefuly on the value on the boundary points.

Code the two-grid method. On the fine grid, apply m times G-S iteration and then restrict the updated residual to the coarse grid. On the coarse grid, use G-S iteration or direct method to solve the equation below the discretization error. Then prolongates the correction to the fine grid and apply additional m G-S iterations.

Use the two-grid method as an iteration to solve the Poisson equation.

Change h from 1/4 to 1/128 and compare the iterations of two-grid methods for different h.

Step 3 V-cycle Multi-grid method

Choose one of the following approach to implement the MG.

(Recrusive way) Apply the two-grid method to the coarse grid problem in Step 2.

(Non-recrusive way) Follow the description of SSC in lecture notes to implement V-cycle.

Use the Vcycle as an iteration to solve the Poisson equation, i.e.,

u = u + Vcycle(r,J); % correction form
u = Vcycle(u,J); % direct update form

Change h from 1/4 to 1/128 and check the iterations and cpu time of MG.

Multigrid on Hierarchical Grids

We consider linear finite element discretization of the Poisson equation on grids obtained by uniform refinement of a coarse grid.

[node,elem] = circlemesh(0,0,1,0.25);
subplot(1,2,1); showmesh(node,elem);
[node,elem] = uniformrefine(node,elem);
subplot(1,2,2); showmesh(node,elem);

 - Min quality 0.8507 - Mean quality 0.9612 - Uniformity 3.93%

Step 1 Hierarchical Meshes

Generate the initial grid by

[node,elem] = circlemesh(0,0,1,0.25);

 - Min quality 0.8507 - Mean quality 0.9612 - Uniformity 3.93%

Refine the initial mesh J times to get the finest mesh. To get a mesh of the disk, the boundary nodes should be projected onto the unit circle.

Construct HB in two ways. Either from the output of uniformrefine during the refinement or call uniformcoarsenred from the finest mesh.

Step 2 Transfer Operator and Smoothers

Assemble the stiffness matrix A in the finest mesh.

Construct prolongation and restriction matrices using HB.

Compute stiffness matrix in each level by the triple product.

Store the smoother tril(A) and triu(A) in each level.

Step 3 V-cycle Multigrid

Follow the lecture notes Introduction to Multigrid method to implement the non-recrusive V-cycle.

Be careful on the boundary nodes. Restrict smoothing to interiori nodes only and enforce the residual on boundary nodes to be zero.

For one single grid, say J = 4, show the decrease of the residual in certain norm for each iteration of the multigrid method.

Test V-cycle MG for J = 3:6. List iteration steps and cpu time.

Algebraic Multigrid Method

We consider solving an SPD matrix equation Ax = b, where A could be obtained as the finite element discretization on a unstructured grids. A coarsening of the graph of A is needed and restriction and prolongation can be constructued based on the coarsening.

Step 1 Matrix

Load the lakemesh.mat in ifem/data.

Assemble the stiffness matrix on this mesh and take the submatrix associated to interior nodes only.

The mesh is only used to generate the matrix. In the later step, only the generated matrix is used.

load lakemesh.mat;
figure; clf; showmesh(node,elem);
A = assemblematrix(node,elem);

Step 2 Coarsening

Use coarsenAMGc to get a set of coarse nodes.

help coarsenAMGc

  COARSENAMGC coarsen the graph of A.
 
  isC = coarsenAMGc(A) terturns a logical array to make a set of nodes as
  the coarse ndoes based on As, a strong connectness matrix modified from
  A. The strong connectness is slightly different with the standard
  definition.
 
  [isC,As] = coarsenAMGc(A,theta) accepts the parameter theta to define the
  strong connectness. The default setting is theta = 0.025. It also outputs
  the strong connectness matrix As which could be used in the constrction
  of prolongation and restriction.
 
  Example
    load lakemesh
    A = assemblematrix(node,elem);
    [isC,As] = coarsenAMGc(A);
 
  See also: coarsenAMGrs, interpolationAMGs, amg
 
  Reference page in Help browser
        <a href="matlab:ifem coarseAMGdoc">coarsenAMGdoc</a> 
 
  Copyright (C) Long Chen. See COPYRIGHT.txt for details.

Step 3 Transfer Operator and Smoothers

Use interpolationAMGs to get restriction and prolongation operators.

help interpolationAMGs

  INTERPOLATIONAMGS construct prolongation and restriction matrices
 
  [Pro,Res] = interpolatoinAMGs(A,isC) construct prolongation and
  restriction matrices use standard matrix-dependent interpolation. 
 
  In the input, A is a SPD matrix and isC is a logical array to indicate
  nodes in coarse matrix. In the output Pro and Res are prolongation and
  restriction matrices satisfying Res = Pro'.
 
  The submatrix A_{cf} is used to construct the interpolation of values on
  fine nodes from that of coarse nodes. The weight is normalized to
  preserve the constant.
 
  Example
    load lakemesh
    A = assemblematrix(node,elem);
    [isC,As] = coarsenAMGc(A);
    [Pro,Res] = interpolationAMGs(As,isC);
 
  See also: coarsenAMGc, amg
 
  Copyright (C) Long Chen. See COPYRIGHT.txt for details.

Step 4 V-cycle Multigrid used with PCG

Follow the Step 3 in part 2 to code a V-cycle. Then use the V-cycle as a preconditioner in PCG.

Test the robustness of the solver, apply uniformrefine to a mesh and generate corresponding matrix. List the iteration steps and CPU time for different size of matrices.