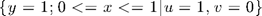Project: Fast Solvers for Stokes Equations

The purpose of this project is to implement fast solvers for solving finite element and finite difference discretization of Stokes equations.

Contents

Part I: Block Preconditioner

Given a triangulation, use codes in Project: Stokes Equation to generate matrices for isoP2-P0 and P1CR-P0 for Stokes equations.

Step 1: Direct solvers in preconditioner

Use [inv(A) 0; 0 inv(Mp)] as the preconditioner and call minres.

Do not form inv(A). Instead the preconditioner can be coded as a subroutine and use backslash to invert A.

For isoP2-P0 and P1CR-P0, the mass matrix for pressure is a diagonal matrix. The inv(Mp) can be realized by a vector multiplication.

Refine the triangulation several times and list the iteration steps of minres and cpu time. The steps should be uniform but the time may not be linear scaled due to the direct solver used in the preconditioner. Use showrate to check the scaling of cpu time vs size of problems.

Step 2: Replace direct solver by multigrid solver

The direct solver of A can be replaced by multigrid solvers included in ifem. Try help mg or help amg.

To use mg, the mesh structure elem should be provided. So you need to modify the matrices to build in the Dirichlet boundary condition. If you only take out submatrices associated to free dofs, you can use amg.

Redo the test in step 1. You should get the same iteration steps and now the cpu time scales linearly.

Step 3: Replace exact multigrid solver by V-cycles

Set option.maxIt = 3 and redo the test. The iteration steps could increase but cpu time is saved instead. How about option.maxIt = 1?

Part II: Block-triangular preconditoner

Use [A B'; 0 -Mp]^{-1} as the preconditioner and call gmres.

Repeat three steps in Part I.

Part III: Multigrid for MAC

Implement Vcycle multigrid for MAC scheme based on DGS smoothing. Refer Project: Multigrid Methods for Poisson equations.

Step 1: Distributive Gauss-Seidel for one level

This is the Part III of Project: MAC Scheme for Stokes Equations. Make sure DGS converges to the correct solution.

Step 2: Transfer operators and two level method

Code the following subroutines

Note: the index map between coarse and fine grids are slightly different for u,v,p. The restriction and prolongation formula can be found in Multigrid Methods for Stokes Equations

Plus presmoothing and one postsmoothing using DGS, you get two level methods. Test your two level methods for different levels. It should convergence in less than 20 steps and indepedent of the number of levels.

Step 3: Vcycle multigrid method

Recrusively apply the two-level method to the coarse grid problem in Step 2.

Redo the test in Step 2.

Part IV: Test Example

Published with MATLAB® 7.14