Crystal growth is a classical example of a phase
transformation from the liquid phase to the solid
phase via heat transfer. A well-known and remarkable
feature observed during the phase transformation
is the occurrence of various patterns and
complex morphologies of the solid/liquid interface
due to the Mullins-Sekerka instability.
The patterns depend on the
initial conditions, the composition of the liquid
phase, the interfacial crystallographic properties,
the supercooling and the applied far-field flux.
Because of its importance, these phase transformations
have received considerable attention from the
materials research community.
Much of this research is concerned with detailed
and extensive studies of dendritic growing shapes.
In many applications (e.g. castings), however,
it is desirable to suppress the Mullins-Sekerka
instability and prevent the formation of dendrites.
This has been much less studied in the literature.
Recently,
Cristini and Lowengrub quantitatively identified conditions for
which the Mullins-Serkerka instability can be suppressed and
compact crystals with controlled shapes can be grown. In 3-D, the conditions are assocated
with a constant heat flux out of the system. Such a condition can be imposed
by appropriately varying the far-field temperature in time.
Using an adaptive 3D boundary integral
method, Cristini and Lowengrub 2
performed nonlinear simulations demonstrating compact crystals can be grown. In
addition, this work also suggested that self-similar growth of non-spherical
crystals is possible.
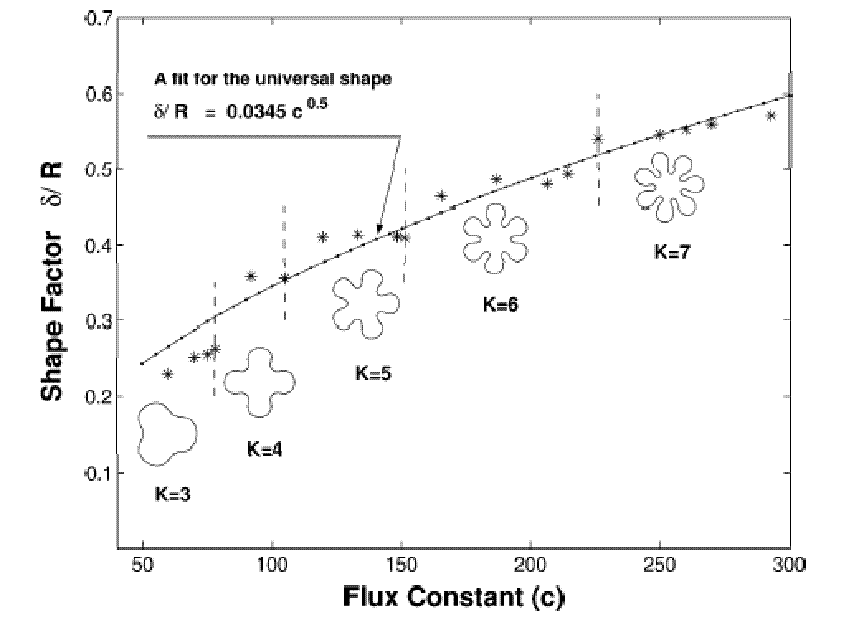
This work was taken to the next level by
S. Li, J.S. Lowengrub, P.H. Leo who demonstrated the existence of 2D self-similar
shapes. Even more importantly and interestingly, it was
demonstrated that there exist universal shape attractors. Namely, for each flux, there
exists a universally attracting shape. This gives the exciting practial possibility of controlling
the shapes of crystals during growth.
Currently, experiments are being performed to test the theory. Additional physical effects
(e.g. solutes) are also being incorporated into the theory.