Multiphase flows

We perform fundamental studies of the behavior of two or more fluids subject to external and internal forces. We are particularly interested in the effect of surface tension on the flow morphology.

Our approach follows two directions:

(1). The development of new, physically-motivated and experimentally validated multiphase flow models;

(2). The development of state-of-the-art adaptive numerical methods;

(1). New physically motivated multiphase flow models

A. Phase-field models. We have been developing new physically based models capable of simulating flows with two or more components with varying miscibilities. A new system of equations, the Navier-Stokes-Cahn-Hilliard System, has been derived. In this approach, related to phase-field models more traditionally used in phase-transformations, sharp interfaces are replaced by narrow transition regions. Concentration fields and corresponding Helmholtz free energies are introduced that characterize the miscibility properties of the components. The concentration fields satisfy a fourth order nonlinear advection-diffusion equation (Cahn-Hilliard) and are coupled to the Navier-Stokes equations through extra reactive stresses that mimic surface tension. Examples of such flows are shown below.

Motion of a compound drop through an interface.



Dripping from a moving nozzle.




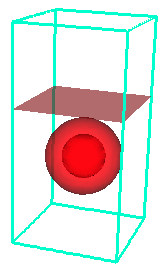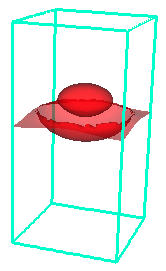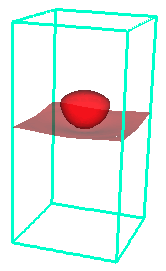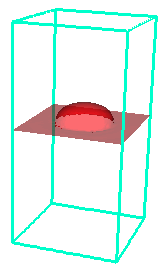
A derivation of the two-phase model can be found in J.S. Lowengrub and L. Truskinovsky, Quasi-incompressible Cahn-Hilliard Fluids and Topological Transitions, Proc. Roy. Soc. London A 454 (1998) 2617-2654. The three-phase model can be found in (J.S. Kim and J.S. Lowengrub, Ternary Cahn-Hilliard fluids, with J.-S. Kim, Int. Free Bound. in review).

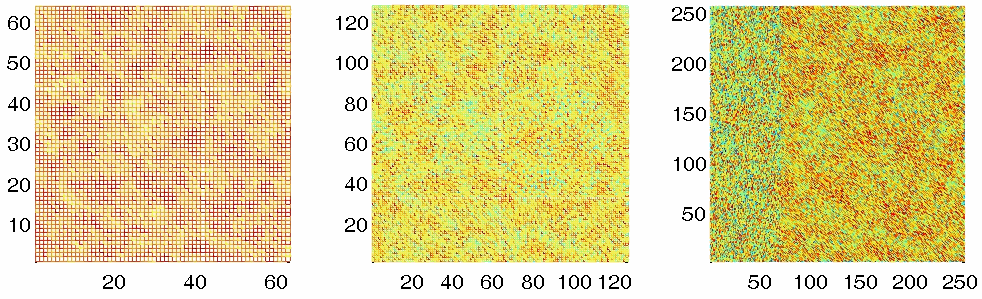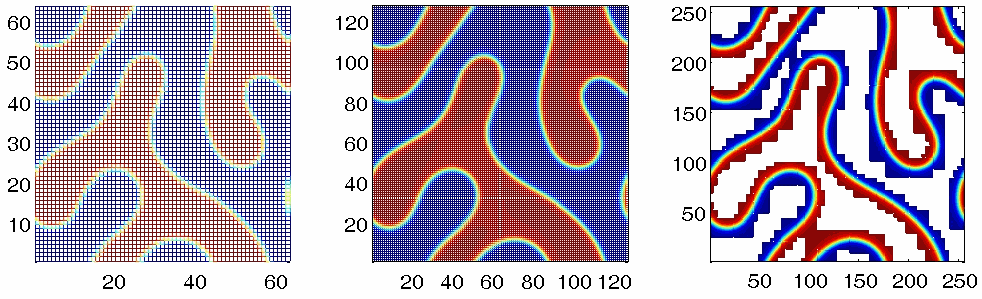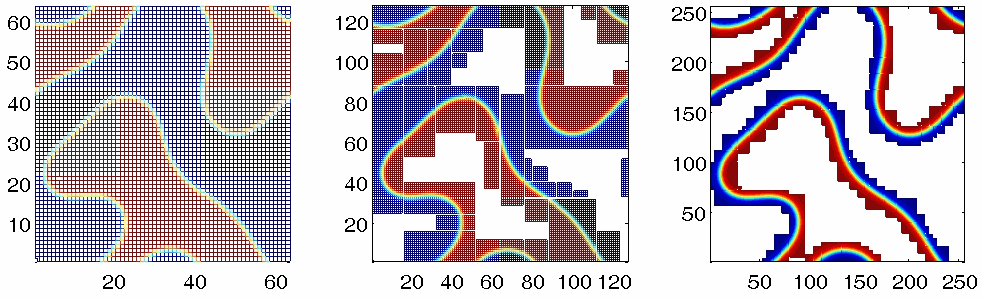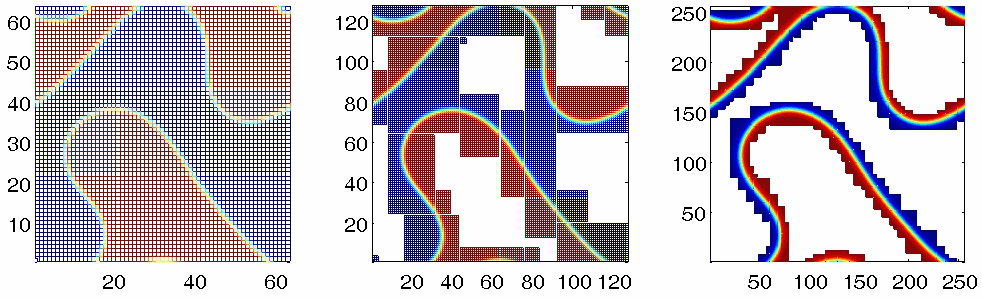
The models are nontrivial to solve as they couple a nonlinear fourth order advection-diffusion equation (Cahn-Hilliard) with the Navier-Stokes equations. To solve the coupled system, we have developed very efficient nonlinear multigrid methods. See for example Conservative multigrid methods for Cahn-Hilliard fluids}, with J.-S. Kim, K. Kang, J. Comp. Phys. 193 (2004) 511-543. We are currently developing adaptive nonlinear multigrid methods for this problem (see below).

Collaborators:

Jun-Seok Kim Ph.D. (2002,UMN)

B. Models of surfactants. We have been developing new physically based models of interfacial flows with surfactants. The key here is to develop an Eulerian approach that can be used together with numerical methods such as the volume-of-fluid or level-set method. The reason for using these methods is that they are capable of capturing topology transitions such as drop-breakup and coalescence. The presence of surfactants has a profound effect on these processes.

Together with Professor Ashley James we have developed a A surfactant conserving volume-of-fluid method for interfacial flows with insoluble surfactant, J. Comp. Phys. 201 (2004) 685-722.

(2). State-of-the-art adaptive numerical methods

A. Unstructured mesh refinement. Very recently, we have developed an adaptive remeshing algorithm for meshes of unstructured triangles in two dimensions and unstructured tetrahedra in three dimensions. The algorithm automatically adjusts the size of the elements with time and position in the computational domain in order to resolve the relevant scales in multiscale physical systems to a user-prescribed accuracy while minimizing computational cost. The optimal mesh that provides the desired resolution is achieved by minimizing a spring-like mesh energy function that depends on the local physical scales using local mesh restructuring operations that include edge-swapping, element insertion/removal, and dynamic mesh-node displacement (equilibration). The algorithm is a generalization to volume domains of the adaptive surface remeshing algorithm developed by Cristini et al., J. Comp. Phys. 168 (2001) 445-463. in the context of deforming interfaces in two and three dimensions.

The algorithm is versatile and can be applied to a number of physical and biological problems, where the local length scales are dictated by the specific problem.

The reference for this work is ( X. Zheng, A. Anderson, J.S. Lowengrub and V. Cristini, Adaptive unstructured volume remeshing algorithms: Application to level-set simulations of multiphase flows, J. Comp. Phys. in review). An example of this approach is shown below.



Drop impacting and rebounding off an interface. Adaptive unstructured mesh.
Comparisons with by recent experiments by Dr. Z. Mohamed-Kassim and Professor Ellen Longmire are shown.
The adaptive mesh is critical to resolving the hydrodynamic repulsive forces in the near contact region. A lack of resolution here will result in a false prediction of coalescence.

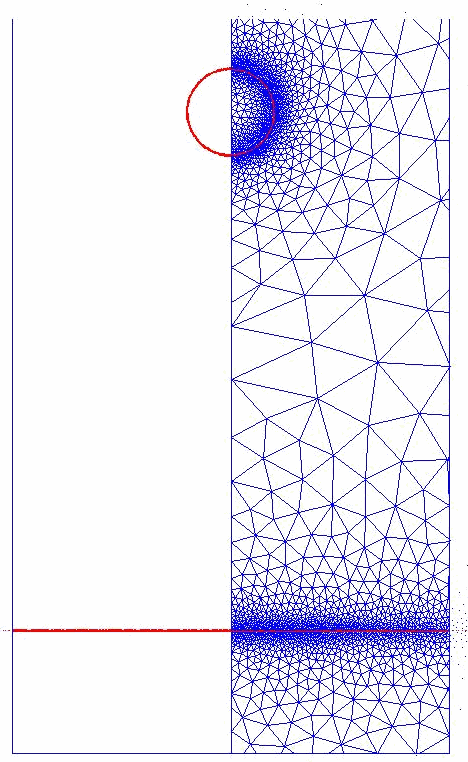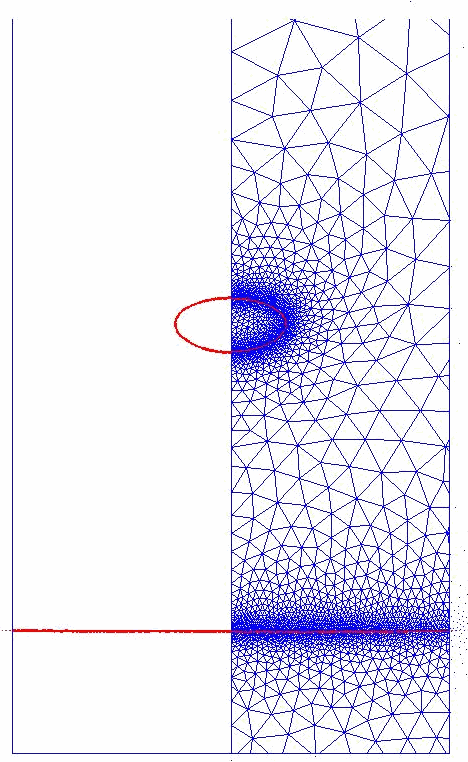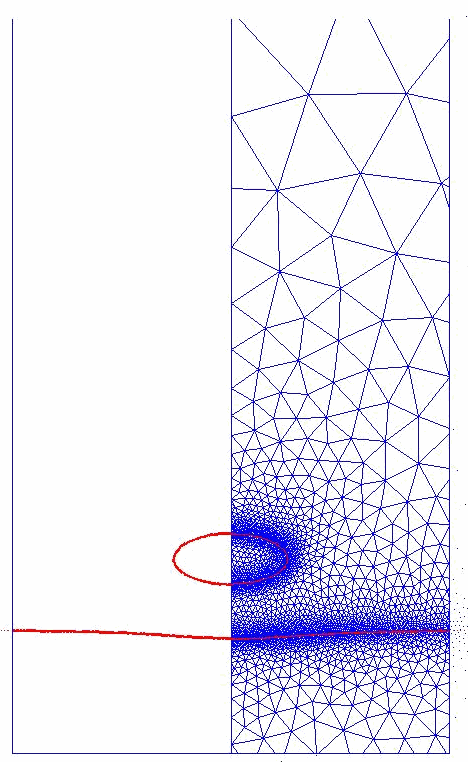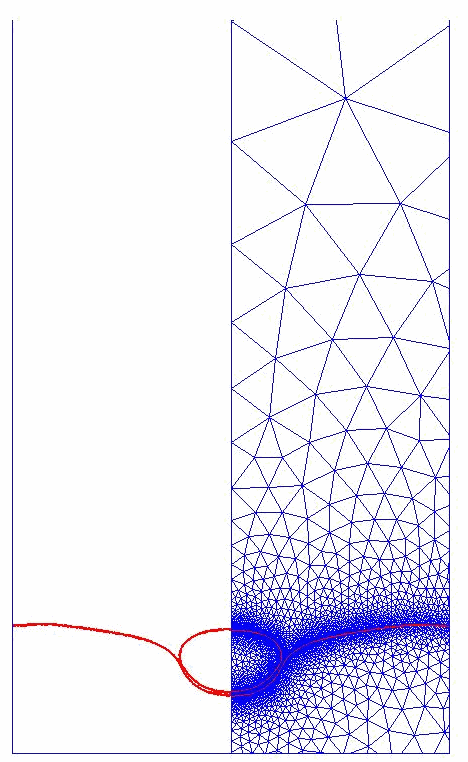
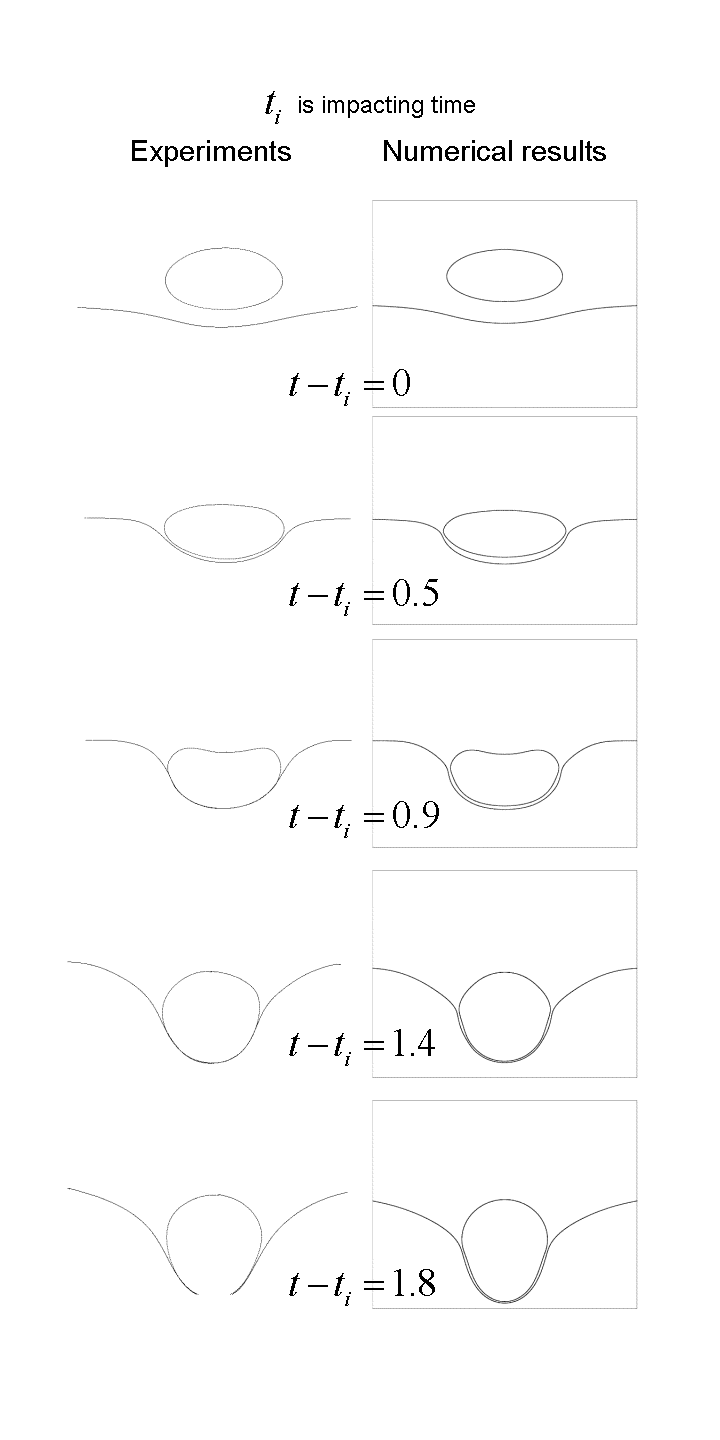
Collaborators:

Xiaoming Zheng (Ph.D. 2005,UCI. Current: U. Michigan) , Tony Anderson (Ph.D. 2008, Northwestern U. (Applied Math Dept), expected), Professor Vittorio Cristini .



B. Structured mesh refinement. We have recently been developing adaptive numerical algorithms using block-structured Cartesian mesh refinement. In this approach, overlapping finite difference Cartesian meshes involving different grid sizes is used to achieve local refinement. We are particularly interested in refining sharp transition regions in the phase-field models. An example is given below.



Coarsening via Cahn-Hilliard Dynamics.
Nonlinear multigrid method using adaptive overlapping Cartesian meshes.
Left: Coarse mesh; Middle: Refined mesh; Right: Finest mesh.

Collaborators:

Jun-Seok Kim Ph.D. (2002,UMN) , and Steven Wise Ph.D.
.