Research interests
I am interested in dynamical systems and the dynamics of nonlinear waves arising in models of physical and biological phenomena. Such systems are typically described by ordinary and partial differential equations (ODEs/PDEs), and I am particularly interested in the development of geometric and analytical techniques to study the bifurcation, existence and stability of emergent waves and patterns in the associated models.
Much of my recent work has focused on systems with widely separated time (or length) scales, or so-called 'fast-slow' systems. These arise ubiquitously in a wide variety of models of natural phenomena; examples include differing timescales in neural or cardiac rhythms, differing spatial scales in astrophysical gas dynamics or long vs. short range interaction in the formation of vegetation patterns. The challenge in studying such systems lies in the fact that the associated equations are singularly perturbed, which can result in remarkably rich and complex dynamics. My approach to these problems draws on dynamical systems tools, including geometric singular perturbation theory, blow-up techniques and canard theory.
My research is supported by the NSF through the grant DMS-2238127 (CAREER).
For information regarding REUs and recent undergraduate research projects, see
undergraduate research.
Recent and ongoing projects
Vegetation pattern formation and dynamics
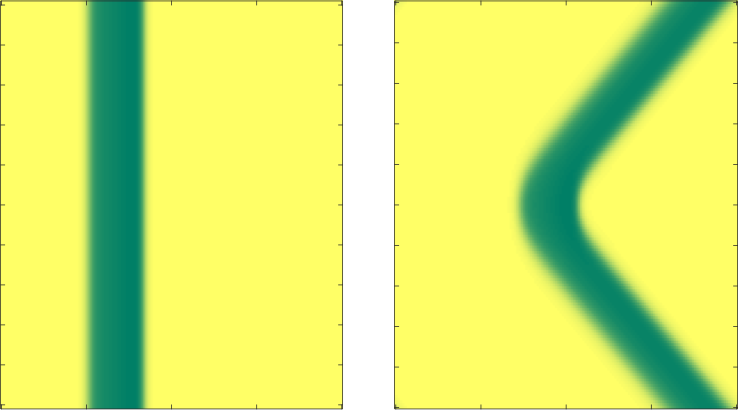
In semiarid regions, limited water resources result in the formation of vegetation patterns. On flat ground, one may observe spots or disorganized labyrinth patterns, while on sloped terrain vegetation can align in resilient stripes or bands. I am especially interesed in the formation of these stripe patterns and their relation to the downhill flow of water. To this end, I am studying a general class of singularly perturbed reaction-diffusion-advection PDE models, and I am focussing on the large advection limit to explain the appearance of spatially localized stripe patterns and the stabilizing effect of downhill advection of water.
Collaborators: R. Bastiaansen, A. Doelman
Single and double pulses in the FitzHugh--Nagumo system
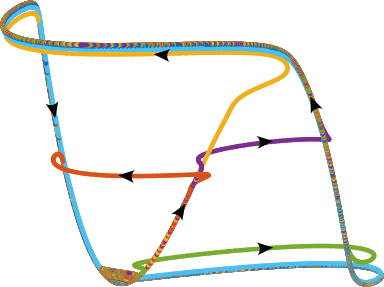
The FitzHugh-Nagumo PDE is a widely studied simplification of the Hodgkin-Huxley equations of mathematical physiology describing nerve axon dynamics. This system admits nerve impulse (or pulse) solutions which travel with fixed speed. We constructed such solutions in a regime in which the tails of the pulses develop small oscillations; upon parameter continuation, these oscillations grow into a second copy of the primary pulse, forming multipulse solutions. We are currently working to extend these methods to the infinite dimensional setting of the spatially discrete FitzHugh-Nagumo system.
Collaborators: H.J. Hupkes, J. Rademacher, B. de Rijk, B. Sandstede
Spike adding systems
Many systems exhibit periodic bursting solutions, comprised of slow phases and active bursting phases which contain a sequence of spikes. Bursting solutions with different numbers of spikes can exist in nearby parameter regimes, and numerical observations suggest that different branches of spiking solutions are connected. I am working to understand mechanisms which result in continuous transitions between solutions with different numbers of spikes and to construct these transitions rigorously.
Patterns and invasion fronts
This projects investigates how invasion processes can select patterns. We focus on the FitzHugh-Nagumo system in a regime where oscillatory patterns can spread into an unstable homogeneous state. The pattern is selected from a family of
periodic wave train solutions by an invasion front which describes
the leading edge of the spreading process.
Collaborators: A. Scheel


