Upcoming REUs
Information about future REU opportunities will be posted here when available.Past REU Projects
Patterns and PDEs (2023): Invasive tumor dynamics

In this project, we analyzed interfaces which appear between healthy tissue and tumor tissue in the context of invasive tumor growth. When viewed as a planar interface in two spatial dimensions, the tumor boundary can exhibit instabilities which result in complex pattern formation along the interface, indicative of more aggressive tumors. We explored this behavior in the context of a reaction diffusion model of acid-mediated tumor growth, using geometric singular perturbation theory, asymptotic methods, and numerical simulations.
Collaborators: A. Doelman, P van Heijster, P Maini
REU Students: Daniel Levy, Erin Okey, Paige Yeung
Publications:
-
P Carter, A Doelman, P van Heijster, D Levy, P Maini, E Okey, P Yeung.
Deformations of acid-mediated invasive tumors in a model with Allee effect. (pdf)
Deformations of acid-mediated invasive tumors in a model with Allee effect. (pdf)
Patterns and PDEs (2022): Wrinkling patterns

In this project during, we explored wrinkling patterns in anisotropic Swift-Hohenberg systems, which have
applications in flexible electronics and materials with tunable surface properties. In particular, we explored the effect of parameters which control the amplitude, wavelength, and orientation of the emerging patterns, using computational approaches.
REU Students: Guogen Lan
Patterns and PDEs (2021): Vegetation fronts

In this project, we investigated traveling fronts which arise as interfaces between desert and vegetatation in semiarid regions. These fronts propagate as the desert invades the vegetated regions. Transverse instabilities in these fronts can cause fingering patterns to appear, which propagate in the opposite direction, allowing the vegetation to re-invade the desert region, providing a possible mechanism for slowing or reversing desertification. We investivated these instabilities using numerical simulation and continuation in the Klausmeier and Gilad models.
Collaborators: A. Doelman
REU Students: Kaitlynn Lilly, Erin Obermayer, Shreyas Rao
Publications:
-
P Carter, A Doelman, K Lilly, E Obermayer, and S Rao.
Criteria for the (in)stability of planar interfaces in singularly perturbed 2-component reaction-diffusion equations.
Physica D 444 (2023), 133596. (preprint, arXiv)
Criteria for the (in)stability of planar interfaces in singularly perturbed 2-component reaction-diffusion equations.
Physica D 444 (2023), 133596. (preprint, arXiv)
Patterns and PDEs (2020): Vegetation spots

In semiarid regions, limited water resources result in the formation of vegetation patterns, and there is evidence that the pattern structure is influenced by topographical conditions. On flat ground, vegetation patches or spot patterns are commonly observed. In this project, using a variant of the Klausmeier reaction-diffusion model of vegetation pattern formation, we analyzed radially symmetric spot patterns using geometric singular perturbation theory and numerical methods.
Collaborators: A. Doelman
REU Students: Ellie Byrnes, Lily Liu
Publications:
-
E Byrnes, P Carter, A Doelman, and L Liu.
Large amplitude radially symmetric spots and gaps in a dryland ecosystem model.
Journal of Nonlinear Science 33(107) (2023). (preprint, arXiv)
Large amplitude radially symmetric spots and gaps in a dryland ecosystem model.
Journal of Nonlinear Science 33(107) (2023). (preprint, arXiv)
Stellar winds (2019)
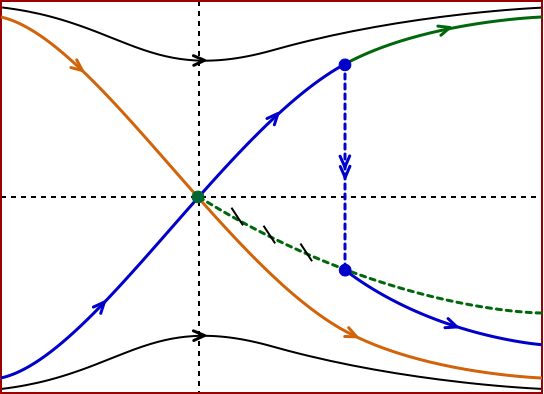
In the setting of viscous stationary spherically symmetric equations of gas dynamics, we are interested in the existence of sub-to-supersonic transitions which describe the phenomena of stellar wind and stellar accretion. These transitions arise as canard solutions in an appropriate fast-slow framework and can be constructed using geometric singular perturbation theory. In this project, we analyzed the effects of viscosity and heat conduction on the structure of stellar winds.
REU Students: Adam Bauer
Publications:
-
A Bauer and P Carter.
Existence of transonic solutions in the stellar wind problem with viscosity and heat conduction.
SIAM Journal on Applied Dynamical Systems 20(1) (2021), pp. 262-298. (preprint)
Existence of transonic solutions in the stellar wind problem with viscosity and heat conduction.
SIAM Journal on Applied Dynamical Systems 20(1) (2021), pp. 262-298. (preprint)
Localized roll patterns (2016)
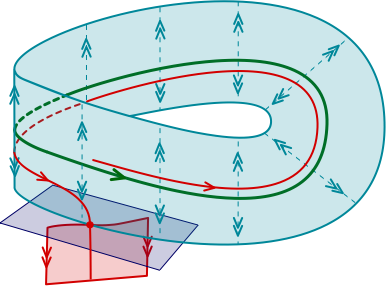
In a project hosted by the Summer@ICERM program in 2016, groups of undergraduate students studied snaking localized roll patterns in the Swift-Hohenberg equation. They analyzed the effect of the underlying geometry/topology of the equation on the structure of the associated snaking curves, as well as implications for higher dimensional patterns.
Collaborators: T. Aougab, M. Beck, J. Bramburger, B. Sandstede
REU Students: Dylan Altschuler, Chloe Avery, Surabhi Desai, Tharathep Sangsawang, Melissa Stadt, Aric Wheeler
Publications:
-
T Aougab, M Beck, P Carter, S Desai, B Sandstede, M Stadt, and A Wheeler.
Isolas versus snaking of localized rolls.
Journal of Dynamics and Differential Equations 31(3) (2019), pp. 1199-1222. (preprint)
-
J Bramburger, D Altschuler, C Avery, T Sangsawang, M Beck, P Carter, and B Sandstede.
Localized radial roll patterns in higher space dimensions.
SIAM Journal on Applied Dynamical Systems 18(3) (2019), pp. 1420-1453. (preprint)
Isolas versus snaking of localized rolls.
Journal of Dynamics and Differential Equations 31(3) (2019), pp. 1199-1222. (preprint)
Localized radial roll patterns in higher space dimensions.
SIAM Journal on Applied Dynamical Systems 18(3) (2019), pp. 1420-1453. (preprint)
Traffic flow (2014/2016)
In this REU project, undergraduate students studied the application of data assimilation to models of traffic flow. In particular, a framework was developed to assimilate both Eulerian (fixed sensor) and Lagrangian (GPS) observations in order to predict traffic states and estimate model parameters. In another project, students applied equaton-free modelling techniques to the study of traffic dynamics.
Collaborators: B. Sandstede, L. Slivinski, C. Xia
REU Students: Tracy Chin, Courtney Cochrane, Joseph DeGuire, Bridget Fan, Emma Holmes, Melissa McGuirl, Patrick Murphy, Jenna Palmer, Jacob Ruth, Clayton Sanford, Rebecca Santorella
Publications:
-
T Chin, J Ruth, C Sanford, R Santorella, P Carter, and B Sandstede.
Enabling equation-free modeling via diffusion maps.
Journal of Dynamics and Differential Equations (2022). (preprint)
-
C Xia, C Cochrane, J DeGuire, G Fan, E Holmes, M McGuirl, P Murphy, J Palmer, P Carter, L Slivinski, and B Sandstede.
Assimilating Eulerian and Lagrangian data in traffic-flow models.
Physica D 346 (2017), pp. 59-72. (preprint)
Enabling equation-free modeling via diffusion maps.
Journal of Dynamics and Differential Equations (2022). (preprint)
Assimilating Eulerian and Lagrangian data in traffic-flow models.
Physica D 346 (2017), pp. 59-72. (preprint)
